题目内容
(山东卷理21)已知函数![]() 其中n∈N*,a为常数.
其中n∈N*,a为常数.
(Ⅰ)当n=2时,求函数f(x)的极值;
(Ⅱ)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
【标准答案】
(I)![]() 的定义域为
的定义域为![]() ,当
,当![]() 时
时![]()
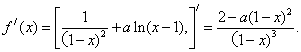
1)当![]() 时,由
时,由![]() 得
得![]()
![]()
当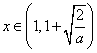 时,
时,![]()
![]() 单调递减;
单调递减;
当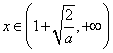 时,
时,![]()
![]() 单调递增。
单调递增。
2)当![]() 时
时![]() 恒成立,
恒成立,![]() 无极值。
无极值。
纵上可知![]() 时,
时,
当![]() 时
时![]() 在
在![]() 处取得极小值为
处取得极小值为![]()
当![]() 时
时![]() 无极值。
无极值。
(II)当![]() 时,
时,![]()
当![]() 时,对任意
时,对任意![]() 恒有
恒有![]() ,故只需证
,故只需证![]() 。
。
令![]() ,
,![]() ,
,
![]()
故![]() 在
在![]() 上单调递增,即
上单调递增,即![]() 在
在![]() 上恒成立,而
上恒成立,而![]()
![]()
![]() 恒成立,
恒成立,
因此,当![]() 时,恒有
时,恒有![]()
【试题分析】:第一问对![]() 讨论时要注意一些显而易见的结果,当
讨论时要注意一些显而易见的结果,当![]() 时
时![]() 恒成立,
恒成立,![]() 无极值。第二问需要对构造的新函数
无极值。第二问需要对构造的新函数![]() 进行“常规处理”,即先证单调性,然后求最值 ,最后作出判断。
进行“常规处理”,即先证单调性,然后求最值 ,最后作出判断。
【高考考点】: 导数及其应用、构造函数证明不等式
【易错提醒】: 没有注意该函数定义域对问题的影响,分类讨论无目标,判断![]() 的正负漏掉符号。
的正负漏掉符号。
【备考提示】: 函数类问题的解题方法要内悟、归纳、整理,使之成为一个系统,在具体运用时自如流畅,既要具有一定的思维定向,也要谨防盲目套用。此类问题对转化能力要求很高,不能有效转化是解题难以突破的主要原因,要善于构造函数证明不等式,从而体现导数的工具性

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目