题目内容
若抛物线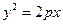
的焦点与椭圆
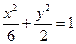的右焦点重合，则
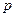的值为（ ﹡ ）
A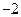． | B． | C． | D． |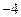
C
解析
练习册系列答案
相关题目
，其右焦点与抛物线
的焦点重合，则e的值为 （ ）
的左右焦点分别为
， 
是以点
为圆心（
为半径的圆与椭圆在第二、三象限的两个交点，且
为等边三角形，则椭圆的离心率
的值是（ ）
与抛物线
相交于P、Q两点，抛物线上一点M与P、Q构成
MPQ的面积为
，这样的点M有且只有（ ）个
,P为抛物线上一点,PA⊥
,那么|PF|= （ ）
，过其焦点且斜率为1的直线交抛物线于
两点，若线段
的中点的纵坐标为2，则该抛物线的标准方程为
设抛物线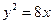
的焦点为
，准线为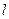
，
为抛物线上一点，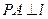
，
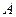为垂足，如果直线
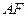斜率为
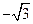，那么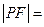
A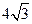． | B．8 | C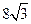． | D．16 |
题目内容
若抛物线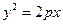的焦点与椭圆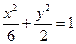的右焦点重合，则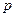的值为（ ﹡ ）
| A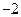． | B． | C． | D． |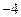
C
解析
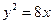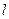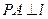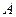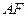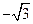设抛物线的焦点为，准线为，为抛物线上一点，，为垂足，如果直线斜率为，那么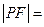
| A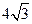． | B．8 | C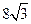． | D．16 |
的左顶点A的斜率为k的直线交椭圆C于另一个点B，且点B在x轴上的射影恰好为右焦点F，若
则椭圆离心率的取值范围是（▲ ）
