Question

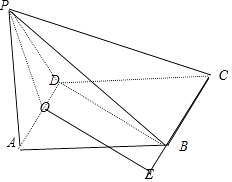
【题目】如图，四棱锥P﹣ABCD的一个侧面PAD为等边三角形，且平面PAD⊥平面ABCD，四边形ABCD是平行四边形，AD=2，AB=4，BD=2
（1）求证；PA⊥BD
（2）求二面角D﹣BC﹣P的余弦值．

Answer 1

【答案】
（1）解：在△ABD中，AD⊥DB，

由平面PAD⊥平面ABCD，∴BD⊥面PAD，∴DB⊥PA

（2）解：二面角D﹣BC﹣P的余弦值即二面角A﹣BC﹣P的余弦值，

作PO⊥AD于O，则PO⊥面ABCD．

过O作OE⊥BC于E，连接PE，则∠PEO为二面角A﹣BC﹣P的平面角．

又△PEO中，PO= ，OE=DB=2 ，故PE= ，

cos∠PEO= ，

∴二面角D﹣BC﹣P的余弦值为 ．

【解析】（1）由面面垂直的性质得BD⊥面PAD，即可证得DB⊥PA．（2）二面角D﹣BC﹣P的余弦值即二面角A﹣BC﹣P的余弦值，作PO⊥AD于O，则PO⊥面ABCD．过O作OE⊥BC于E，连接PE，则∠PEO为二面角A﹣BC﹣P的平面角，在△PEO中，求得cos∠PEO= ，即可得二面角D﹣BC﹣P的余弦值
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点，需要掌握垂直于同一个平面的两条直线平行才能正确解答此题．