题目内容
已知复数z=（1+2m）+（3+m）i，（m∈R）．（1）若复数z在复平面上所对应的点在第二象限，求m的取值范围；
（2）求当m为何值时，|z|最小，并求|z|的最小值．
【答案】分析：（1）复数z在复平面上所对应的点在第二象限，应实部小于0，虚部大于0．
（2）根据复数模的计算公式，得出关于m的函数求出最小值．
解答：解：（1）由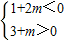
解得-3＜m＜-
．
（2）|z|2=（1+2m）2+（3+m）2
=5m2+10m+10
=5（m+1）2+5
所以当m=-1时，即|m|2min=5．
|z|的最小值为：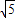
．
点评：本题考查复数的分类、几何意义、模的计算、函数思想与考查计算能力．
（2）根据复数模的计算公式，得出关于m的函数求出最小值．
解答：解：（1）由
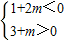
解得-3＜m＜-
．（2）|z|2=（1+2m）2+（3+m）2
=5m2+10m+10
=5（m+1）2+5
所以当m=-1时，即|m|2min=5．
|z|的最小值为：
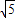．点评：本题考查复数的分类、几何意义、模的计算、函数思想与考查计算能力．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
已知复数z满足（2-i）z=5（i为虚数单位）则|z|=（ ）
A、
| ||
| B、3 | ||
| C、2 | ||
| D、1 |