题目内容
设F(x)＝f(x)－g(x),其中f(x)＝lg(x－1),并且仅当(x0,y0)在y＝lg(x－1)的图象上时，(2x0,2y0)在y＝g(x)的图象上。
（1） 写出g(x)的函数解析式
（2） 当x在什么区间时，F(x)≥0？
【答案】
解: (1)设2x0＝X,2y0＝Y那么
x0＝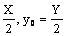
∵ f(x)＝lg(x－1)
且 (x0,y0)在y＝lg(x－1)的图象上， ∴ y0＝lg(x0－1)
∴ 
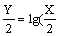－1) 即 Y＝2lg(
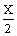－1)
∵ (2x0,2y0)在y＝g(x)的图象上，
∴ g(x)＝2lg(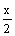
－1)
(2)F(x)＝lg(x－1)－2lg(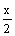－1)
由题意得，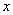
需满足 lg(x－1)－2lg(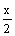－1)≥0
上面的不等式等价于
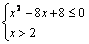Û
Û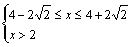
Û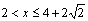
∴ 当x∈(2,4＋2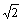
]时，F(x)≥0.
练习册系列答案
相关题目
，
(a＞0且a≠1)．
有两个不等实根，求实数m的范围；
恒成立，求实数m的范围．
x0∈R，使得
sinx0＋
cosx0＞1；
)，则
x∈(－
，
)，必有f(x)＜f(x＋0.1)；
)，则函数y＝f(x＋
)是奇函数；
)＝2sin(2x＋
)．
(x)的图象经过点(
，0)，(2，0)，如图所示．
sinxcosx
)＋K(A＞0，ω＞0，0＜
)的形式，并求出f(x)的最小正周期；
，求tanα的值．