题目内容
函数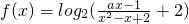 在x∈[1,3]上恒有意义,则实数a的取值范围是________.
在x∈[1,3]上恒有意义,则实数a的取值范围是________.
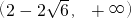
分析:由
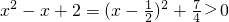 可原不等式可转化ax-1>-2x2+2x-4即
可原不等式可转化ax-1>-2x2+2x-4即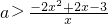 =
=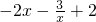 在x∈[1,3]上恒成立,构造函数g(x)=
在x∈[1,3]上恒成立,构造函数g(x)=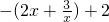 ,利用基本不等式可求函数g(x)的最大值,a>g(x)max即可
,利用基本不等式可求函数g(x)的最大值,a>g(x)max即可解答:由题意可得,
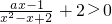 在[1,3]恒成立
在[1,3]恒成立由于
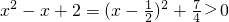
ax-1>-2x2+2x-4
1≤x≤3
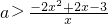 =
=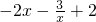 在x∈[1,3]上恒成立
在x∈[1,3]上恒成立令g(x)=
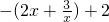
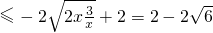
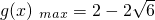
由
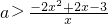 =
=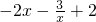 在x∈[1,3]上恒成立可得a
在x∈[1,3]上恒成立可得a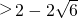
故答案为:
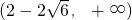
点评:本题以对数函数的定义域的恒成立为切入点,主要考查了函数的 参数的范围,此类问题一般是转化为求解函数的最值,若a>f(x)恒成立?a>f(x)max;a<f(x)恒成立?a<f(x)min,还要注意基本不等式在最值求解中的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
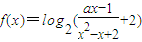 在x∈[1,3]上恒有意义,则实数a的取值范围是 .
在x∈[1,3]上恒有意义,则实数a的取值范围是 .