题目内容
已知函数 ,
, 且
且 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)判断并证明函数 在区间
在区间 上的单调性.
上的单调性.
【答案】
(Ⅰ) (Ⅱ)单调递增
(Ⅱ)单调递增
【解析】
试题分析:(Ⅰ)利用 得出
得出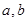 的关系,再根据
的关系,再根据 得出
得出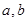 的值,属于待定系数法;
的值,属于待定系数法;
(Ⅱ)利用单调性的定义取值--作差--定号--判断,证明.
试题解析:(Ⅰ)因为 ,
, ,由
,由 ,
, ,又
,又 ,
, ,
, ,
, .(5分)
.(5分)
(Ⅱ)由(1)得 ,函数在
,函数在 单调递增。
单调递增。
证明:任取 且
且 ,
,

 (8分)
(8分)
 ,
,
 (10分)
(10分)
即 ,故函数
,故函数 在
在 上单调递增 (12分)
上单调递增 (12分)
考点:如何求参数,单调性的证明.

练习册系列答案
相关题目
 ,且
,且 在
在 和
和 处取得极值.
处取得极值. ,是否存在实数
,是否存在实数 ,使得曲线
,使得曲线 与
与 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出
 ,且
,且
 的值
的值 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明 ,若
,若 且
且 ,则下列不等式中正确的是( )
,则下列不等式中正确的是( ) B.
B.
 C.
C.
 D.
D.
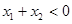
 ,且
,且 ,
, .那么下列命题中真命题的序号是
.那么下列命题中真命题的序号是 的最大值为
的最大值为 ②
②  在
在 上是减函数
④
上是减函数
④ 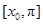 上是减函数
上是减函数 ,且
,且 是奇函数。
是奇函数。 ,
, 的值;
的值; 的单调区间。
的单调区间。