题目内容
求经过点(2,0)且与y=| 1 | x |
分析:设出直线方程,通过联立方程组,判别式为0,即可用点斜式求出切线方程.
解答:解:设切线方程为y=k(x-2),所以
因为相切所以△=0,解得k=0或k=-1,
∴切线方程为x+y-2=0.或y=0
|
∴切线方程为x+y-2=0.或y=0
点评:此题主要考查了直线的点斜式,直线与曲线相切关系的应用,比较简单.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 相切的直线方程.
相切的直线方程. 曲线相切的直线方程.
曲线相切的直线方程.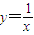 曲线相切的直线方程.
曲线相切的直线方程.