题目内容
求经过点(2,0)且与曲线 相切的直线方程.
相切的直线方程.
【答案】
x+y-2=0.
【解析】
试题分析:可以验证点(2,0)不在曲线上,故设切点为 .
.
由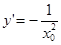 得所求直线方程为
得所求直线方程为
 .
.
由点(2,0)在直线上,得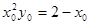 ,
,
再由 在曲线上,得
在曲线上,得 ,
,
联立可解得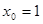 ,
,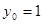 .所求直线方程为x+y-2=0.
.所求直线方程为x+y-2=0.
考点:本题主要考查导数的运算及导数的几何意义。
点评:在点P处的切线斜率就是函数在该点的导数值。求过“点”的切线方程,应注意点是否在曲线上。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 曲线相切的直线方程.
曲线相切的直线方程.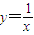 曲线相切的直线方程.
曲线相切的直线方程.