题目内容
若非零向量 、
、 ,满足
,满足 ,且
,且 ,则
,则 与
与 的夹角大小为 .
的夹角大小为 .
【答案】分析:设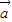 与
与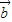 的夹角大小为θ,由题意得2
的夹角大小为θ,由题意得2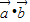 +
+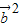 =2
=2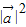 cosθ+
cosθ+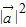 =0,由此求得 cosθ 的值,即可得到
=0,由此求得 cosθ 的值,即可得到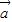 与
与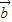 的夹角θ的大小.
的夹角θ的大小.
解答:解:设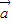 与
与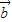 的夹角大小为θ,由题意
的夹角大小为θ,由题意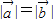 ,
,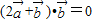 可得2
可得2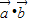 +
+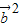 =2|
=2|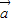 ||
||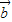 |cosθ+
|cosθ+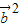 =2
=2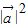 cosθ+
cosθ+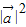 =0,
=0,
解得 cosθ=- .
.
再由0≤θ≤π可得,θ=120°,
故答案为120°.
点评:本题主要考查两个向量的数量积的定义,两个向量垂直的性质,根据三角函数的值求角,属于中档题.
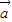 与
与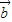 的夹角大小为θ,由题意得2
的夹角大小为θ,由题意得2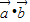 +
+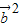 =2
=2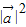 cosθ+
cosθ+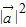 =0,由此求得 cosθ 的值,即可得到
=0,由此求得 cosθ 的值,即可得到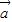 与
与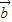 的夹角θ的大小.
的夹角θ的大小.解答:解:设
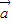 与
与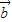 的夹角大小为θ,由题意
的夹角大小为θ,由题意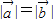 ,
,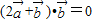 可得2
可得2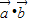 +
+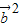 =2|
=2|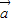 ||
||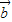 |cosθ+
|cosθ+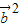 =2
=2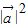 cosθ+
cosθ+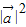 =0,
=0,解得 cosθ=-
 .
.再由0≤θ≤π可得,θ=120°,
故答案为120°.
点评:本题主要考查两个向量的数量积的定义,两个向量垂直的性质,根据三角函数的值求角,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 、
、 ,满足
,满足 ,且
,且 ,则
,则 R,
R, ”的否定是“
”的否定是“ ”;
”; ②若
②若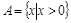 ,
, ,则
,则 ( RB)=A;
( RB)=A; 是偶函数的充要条件是
是偶函数的充要条件是 (
( Z);
Z); b,b=
b,b= R),则
R),则 .
.