题目内容
给出下列4个命题:
①函数f(x)=x|x|+ax+m是奇函数的充要条件是m=0:
②若函数f(x)=log(ax+1)的定义域是{x|x<l},则a<-1;
③若loga2<logb2,则
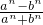 =1(其中n∈N+);
=1(其中n∈N+);
④圆:x2+y2-10x+4y-5=0上任意点M关于直线ax-y-5a=2的对称点,M′也在该圆上填上所有正确命题的序号是 ________.
①,④
分析:依据各选项中的已知条件,逐一分析各个各个选项是否正确,把正确的选项找出来,填在横线上.
解答:①函数f(x)的定义域是实数集R,关于原点对称,此函数奇函数的充要条件是f(-x)=-f(x),
即-x|x|-ax+m=-x|x|-ax-m,即 m=0,故①正确.
②函数f(x)=log(ax+1)的定义域是{x|x<l},故 a<0,且ax+1>0的解集是x<l,故只有 a=-1,
故②不正确.
③∵loga2<logb2,∴a>b>1,或者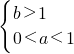 ,
,
当a>b>1时,则
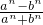 =
=
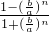 =
=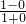 =1,
=1,
当 b>1 且 0<a<1时,则
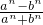 =
=
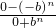 =(-1)n=±1,
=(-1)n=±1,
故③不正确.
④圆:x2+y2-10x+4y-5=0 即 (x-5)2+(y+2)2=34,圆心为(5,-2)
直线ax-y-5a=2 即a(x-5)-y-2=0,此直线过定点(5,-2),即圆的圆心,故圆:x2+y2-10x+4y-5=0 关于此直线
对称,故④正确.
综上,①④正确,②③不正确,
故答案为 ①④.
点评:本题考查函数的奇偶性、定义域、直线过定点、点关于直线对称,以及极限的运算,体现了等价转化和分类讨论的数学思想.
分析:依据各选项中的已知条件,逐一分析各个各个选项是否正确,把正确的选项找出来,填在横线上.
解答:①函数f(x)的定义域是实数集R,关于原点对称,此函数奇函数的充要条件是f(-x)=-f(x),
即-x|x|-ax+m=-x|x|-ax-m,即 m=0,故①正确.
②函数f(x)=log(ax+1)的定义域是{x|x<l},故 a<0,且ax+1>0的解集是x<l,故只有 a=-1,
故②不正确.
③∵loga2<logb2,∴a>b>1,或者
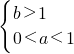 ,
,当a>b>1时,则

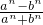 =
=
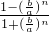 =
=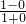 =1,
=1,当 b>1 且 0<a<1时,则

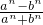 =
=
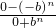 =(-1)n=±1,
=(-1)n=±1,故③不正确.
④圆:x2+y2-10x+4y-5=0 即 (x-5)2+(y+2)2=34,圆心为(5,-2)
直线ax-y-5a=2 即a(x-5)-y-2=0,此直线过定点(5,-2),即圆的圆心,故圆:x2+y2-10x+4y-5=0 关于此直线
对称,故④正确.
综上,①④正确,②③不正确,
故答案为 ①④.
点评:本题考查函数的奇偶性、定义域、直线过定点、点关于直线对称,以及极限的运算,体现了等价转化和分类讨论的数学思想.

练习册系列答案
相关题目