题目内容
一动圆与圆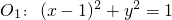 外切,与圆
外切,与圆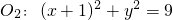 内切.
内切.
(I)求动圆圆心M的轨迹L的方程.
(Ⅱ)设过圆心O1的直线l:x=my+1与轨迹L相交于A、B两点,请问△ABO2(O2为圆O2的圆心)的内切圆N的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
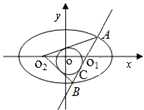 解:(1)设动圆圆心为M(x,y),半径为R.
解:(1)设动圆圆心为M(x,y),半径为R.由题意,动圆与圆
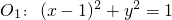 外切,与圆
外切,与圆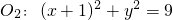 内切∴|MO1|=R+1,|MO2|=3-R,∴|MO1|+|MO2|=4. (3分)
内切∴|MO1|=R+1,|MO2|=3-R,∴|MO1|+|MO2|=4. (3分)由椭圆定义知M在以O1,O2为焦点的椭圆上,且a=2,c=1,
∴b2=a2-c2=4-1=3.
∴动圆圆心M的轨迹L的方程为
 . (6分)
. (6分)(2)如图,设△ABO2内切圆N的半径为r,与直线l的切点为C,则三角形△ABO2的面积
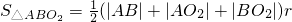 =
=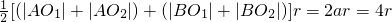
当
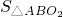 最大时,r也最大,△ABO2内切圆的面积也最大,(7分)
最大时,r也最大,△ABO2内切圆的面积也最大,(7分)设A(x1,y1)、B(x2,y2)(y1>0,y2<0),
则
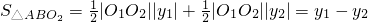 ,(8分)
,(8分)由
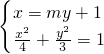 ,得(3m2+4)y2+6my-9=0,
,得(3m2+4)y2+6my-9=0,解得
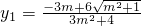 ,
,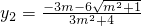 ,(10分)
,(10分)∴
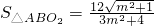 ,令
,令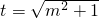 ,则t≥1,且m2=t2-1,
,则t≥1,且m2=t2-1,有
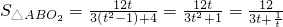 ,令
,令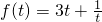 ,则
,则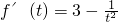 ,
,当t≥1时,f'(t)>0,f(t)在[1,+∞)上单调递增,有f(t)≥f(1)=4,
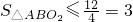 ,
,即当t=1,m=0时,4r有最大值3,得
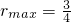 ,这时所求内切圆的面积为
,这时所求内切圆的面积为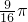 ,
,∴存在直线l:x=1,△ABO2的内切圆M的面积最大值为
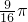 .(14分)
.(14分)分析:(1)利用动圆与圆
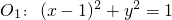 外切,与圆
外切,与圆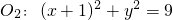 内切,可得|MO1|=R+1,|MO2|=3-R,∴|MO1|+|MO2|=4,由椭圆定义知M在以O1,O2为焦点的椭圆上,从而可得动圆圆心M的轨迹L的方程;
内切,可得|MO1|=R+1,|MO2|=3-R,∴|MO1|+|MO2|=4,由椭圆定义知M在以O1,O2为焦点的椭圆上,从而可得动圆圆心M的轨迹L的方程;(2)当
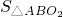 最大时,r也最大,△ABO2内切圆的面积也最大,表示出三角形的面积,利用换元法,结合导数,求得最值,即可求得结论.
最大时,r也最大,△ABO2内切圆的面积也最大,表示出三角形的面积,利用换元法,结合导数,求得最值,即可求得结论.点评:本题考查轨迹方程的求法,考查椭圆的定义,考查学生分析解决问题的能力,解题的关键是正确运用椭圆的定义,确定
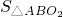 最大时,r也最大,△ABO2内切圆的面积也最大
最大时,r也最大,△ABO2内切圆的面积也最大 
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
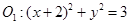 外切,与圆
外切,与圆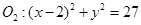 内切.
内切.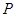 ,使直线
,使直线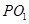 与
与 的斜率
的斜率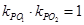 ?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)
?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)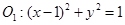 外切,与圆
外切,与圆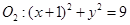 内切.
内切.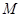 的轨迹
的轨迹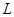 的方程;
的方程;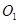 的直线
的直线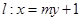 与轨迹
与轨迹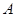 、
、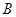 两点,请问
两点,请问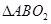 (
(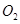 为圆
为圆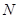 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线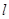 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. 外切,与圆
外切,与圆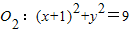 内切.
内切.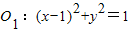 外切,与圆
外切,与圆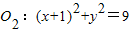 内切.
内切.