题目内容
一动圆与圆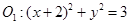 外切,与圆
外切,与圆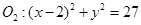 内切.
内切.
(I)求动圆圆心M的轨迹方程.(II)试探究圆心M的轨迹上是否存在点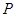 ,使直线
,使直线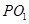 与
与 的斜率
的斜率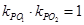 ?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)
?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)
【答案】
(I) 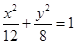 (II) 圆心M的轨迹上存在四个点
(II) 圆心M的轨迹上存在四个点 ,使直线
,使直线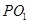 与
与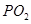 的斜率
的斜率 .
.
【解析】解:(1)设动圆圆心为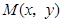 ,半径为
,半径为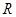 .
.
由题意,得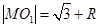 ,
,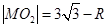 ,
(1分)
,
(1分)
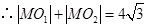 , 由椭圆定义知
, 由椭圆定义知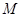 在以
在以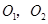 为焦点的椭圆上, (3分)
为焦点的椭圆上, (3分)
且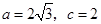 ,
,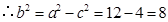 .
(5分)
.
(5分)
 动圆圆心M的轨迹方程为
动圆圆心M的轨迹方程为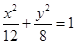 . (6分)
. (6分)
(II) 由(I)知动圆圆心M的轨迹是椭圆,它的两个焦点坐标分别为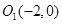 和
和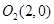 (7分)
(7分)
设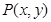 是椭圆上的点,由
是椭圆上的点,由 得
得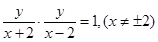 (9分)
(9分)
即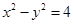
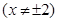 ,这是实轴在
,这是实轴在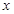 轴,顶点是椭圆的两个焦点的双曲线,它与椭圆的交点即为点P。由于双曲线的两个顶点在椭圆内,根据椭圆和双曲线的对称性可知,它们必有四个交点.
轴,顶点是椭圆的两个焦点的双曲线,它与椭圆的交点即为点P。由于双曲线的两个顶点在椭圆内,根据椭圆和双曲线的对称性可知,它们必有四个交点.
即圆心M的轨迹上存在四个点 ,使直线
,使直线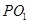 与
与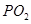 的斜率
的斜率 . (12分)
. (12分)

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
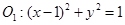 外切,与圆
外切,与圆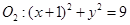 内切.
内切. 的轨迹
的轨迹 的方程;
的方程; 的直线
的直线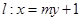 与轨迹
与轨迹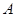 、
、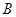 两点,请问
两点,请问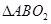 (
(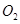 为圆
为圆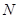 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线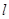 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.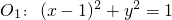 外切,与圆
外切,与圆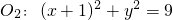 内切.
内切. 外切,与圆
外切,与圆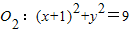 内切.
内切.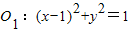 外切,与圆
外切,与圆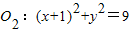 内切.
内切.