题目内容
已知双曲线的两个焦点为F1(-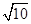 ,0)、F2(
,0)、F2(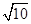 ,0),M是此双曲线上的一点,且满足
,0),M是此双曲线上的一点,且满足 ·
·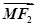 =0,|
=0,| |·|
|·|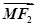 |=2,则该双曲线的方程是 .
|=2,则该双曲线的方程是 .
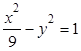
解析试题分析:由于三角形PF1F2为直角三角形,故 ,所以(MF1-MF2)2+2MF1•MF2=40,由双曲线定义得(2a)2+4=40,即a2=9,故b2=1,所以双曲线方程为
,所以(MF1-MF2)2+2MF1•MF2=40,由双曲线定义得(2a)2+4=40,即a2=9,故b2=1,所以双曲线方程为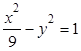 .故答案为:
.故答案为: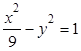 .
.
考点:双曲线的标准方程.

练习册系列答案
相关题目
题目内容
已知双曲线的两个焦点为F1(-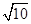 ,0)、F2(
,0)、F2(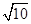 ,0),M是此双曲线上的一点,且满足
,0),M是此双曲线上的一点,且满足 ·
·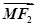 =0,|
=0,| |·|
|·|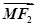 |=2,则该双曲线的方程是 .
|=2,则该双曲线的方程是 .
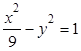
解析试题分析:由于三角形PF1F2为直角三角形,故 ,所以(MF1-MF2)2+2MF1•MF2=40,由双曲线定义得(2a)2+4=40,即a2=9,故b2=1,所以双曲线方程为
,所以(MF1-MF2)2+2MF1•MF2=40,由双曲线定义得(2a)2+4=40,即a2=9,故b2=1,所以双曲线方程为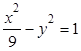 .故答案为:
.故答案为: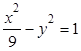 .
.
考点:双曲线的标准方程.
