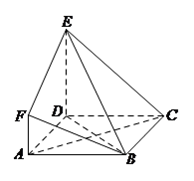题目内容
【题目】如图,直三棱柱 ![]() 中,
中, ![]() 分别是
分别是 ![]() 的中点,
的中点, ![]() .
.
(Ⅰ)证明: ![]() ∥平面
∥平面 ![]() ;
;
(Ⅱ)求锐二面角 ![]() 的余弦值.
的余弦值.
【答案】解:
(Ⅰ)连结 ![]() ,交
,交 ![]() 于点
于点 ![]() ,连结
,连结 ![]() ,则
,则 ![]() 为
为 ![]() 的中点,因为
的中点,因为 ![]() 为
为 ![]() 的中点,所以
的中点,所以 ![]() ∥
∥ ![]() ,又因为
,又因为 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() ∥平面
∥平面 ![]()
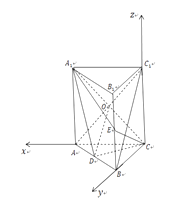
(Ⅱ)由 ![]() ,可知
,可知 ![]() ,以
,以 ![]() 为坐标原点,
为坐标原点, ![]() 方向为
方向为 ![]() 轴正方向,
轴正方向, ![]() 方向为
方向为 ![]() 轴正方向,
轴正方向, ![]() 方向为
方向为 ![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系 ![]() ,
,
则 ![]() ,
,
![]() ,
, ![]() ,
, ![]()
设 ![]() 是平面
是平面 ![]() 的法向量,则
的法向量,则 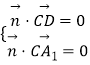 即
即 ![]()
可取 ![]() .
.
同理,设 ![]() 是平面
是平面 ![]() 的法向量,则
的法向量,则 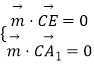 ,
,
可取 ![]() .从而
.从而 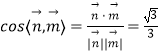
所以锐二面角 ![]() 的余弦值为
的余弦值为 ![]()
【解析】(I)证明线面平行,关键是证明线面平行,因此连结 ![]() ,交
,交 ![]() 于点 O,再利用三角形相似即可。
于点 O,再利用三角形相似即可。
(II)在空间求二面角,我们一般是建系求点,得法向量,再应用夹角公式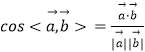 即可。
即可。
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
相关题目