题目内容
设函数
（I）求函数的单调区间；
（II）求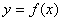
在[0，
]
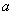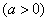上的最小值；
（III）当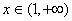
时，证明：对任意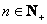
【答案】
解：（I）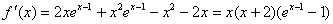
…………2分
令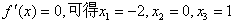
|
|
|
—2 |
（-2，0） |
0 |
（0，1） |
1 |
|
|
|
— |
0 |
+ |
0 |
— |
0 |
+ |
|
|
减 |
极小 |
增 |
极大 |
减 |
极小 |
增 |
函数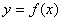
的增区间为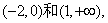
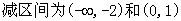…………5分
（II）①当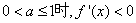
， 
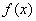在
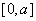上递减，
.
②当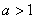
时，由（I）知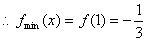
在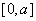上的最小值是
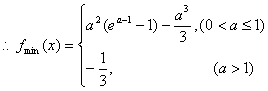………………8分
（III）设
；……………………… 10分
即当
时，不等式成立。
所以当
时，
………………14分
练习册系列答案
相关题目
确定数列
，
，函数
能确定数列
，
，若对于任意
都有
，则称数列
，若由函数
确定的数列
；
的前n项和
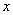
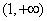
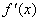
，写出
表达式，并证明你的结论；
，当
时，设
，
是数列
的前
项和，且
恒成立，求
的取值范围. 
轴的交点也在函数
的图象上，且在此点处有公切线。
的大小。