题目内容
如图, 是边长为2的正三角形,若
是边长为2的正三角形,若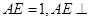 平面
平面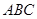 ,平面
,平面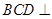 平面
平面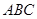 ,
,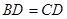 ,且
,且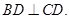
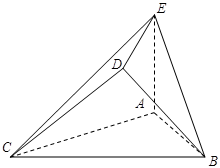
(Ⅰ)求证: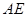 //平面
//平面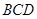 ;
;
(Ⅱ)求证:平面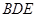
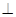 平面
平面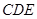 。
。
(Ⅰ)详见解析,(Ⅱ)详见解析
解析试题分析:(Ⅰ)要证线面平行,需有线线平行 观察可知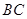 的中点
的中点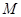 与
与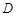 连线平行于
连线平行于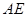 有了方向,要实现目标,还需证明 题目中垂直条件较多,就从垂直关系上证平行 由平面
有了方向,要实现目标,还需证明 题目中垂直条件较多,就从垂直关系上证平行 由平面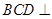 平面
平面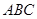 ,
,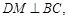 根据面面垂直性质定理推出
根据面面垂直性质定理推出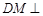 平面
平面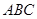 ,而
,而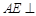 平面
平面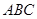 ,从而得到
,从而得到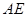
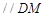 ,(Ⅱ)
,(Ⅱ)
要证面面垂直,需有线面垂直 由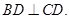 易得证明方向为
易得证明方向为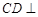 面
面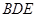 ,或
,或 面
面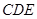 ,而由(1)知
,而由(1)知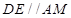 ,而正三角形中
,而正三角形中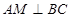 ,因此只需证
,因此只需证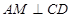 ,而由
,而由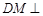 平面
平面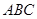 易得
易得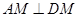 ,从而
,从而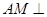 面
面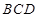 ,也即有
,也即有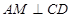
试题解析:证明:(1) 取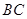 的中点
的中点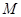 ,连接
,连接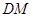 、
、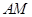 ,
,
因为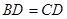 ,且
,且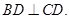
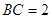 2分
2分
所以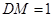 ,
,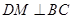 ,
,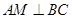 3分
3分
又因为平面 ⊥平面
⊥平面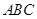 ,
,
所以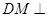 平面
平面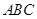
所以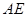 ∥
∥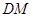 , 4分
, 4分
又因为 平面
平面 ,
,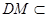 平面
平面 , 5分
, 5分
所以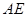 ∥平面
∥平面 6分
6分
(2)由(1)已证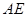 ∥
∥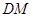 ,又
,又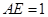 ,
,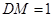 ,
,
所以四边形 是平行四边形,
是平行四边形,
所以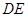 ∥
∥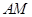 8分
8分
由(1)已证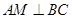 ,又因为平面
,又因为平面 ⊥平面
⊥平面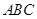 ,
,
所以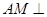 平面
平面 ,
,
所以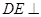 平面
平面
又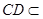 平面
平面 ,所以
,所以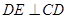 10分
10分
因为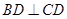 ,
,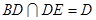 ,
,
所以

练习册系列答案
相关题目
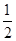 AB=1,M是PB的中点.
AB=1,M是PB的中点.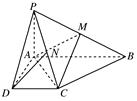
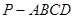 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,
, 为
为 中点.
中点.
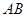 //平面
//平面 ;
; 平面
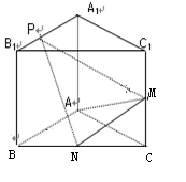
平面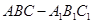 的侧棱与底面垂直,
的侧棱与底面垂直,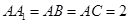 ,
,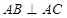 , M、N分别是
, M、N分别是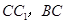 的中点,点P在线段
的中点,点P在线段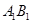 上,且
上,且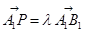 ,
,
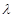 取何值,总有
取何值,总有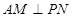 .
.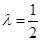 时,求平面
时,求平面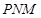 与平面
与平面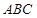 所成锐二面角的余弦值.
所成锐二面角的余弦值.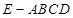 中,底面
中,底面 是正方形,
是正方形,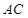 与
与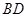 交于点
交于点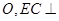 底面
底面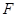 为
为 的中点.
的中点.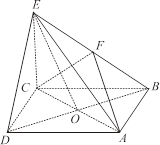
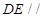 平面
平面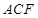 ;
; ,在线段
,在线段 上是否存在点
上是否存在点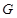 ,使
,使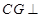 平面
平面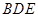 ?若存在,求出
?若存在,求出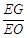 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.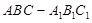 中,
中,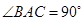 ,
,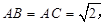
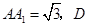 是
是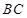 中点,
中点,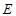 是
是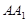 中点.
中点.
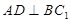 ;
;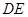 ∥面
∥面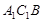 .
.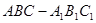 中,
中, ,
, ,异面直线
,异面直线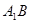 与
与 所成的角等于
所成的角等于 ,设
,设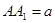 .
.
 的值;
的值; 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小.
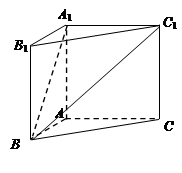
 的底面是边长为
的底面是边长为 的正三角形,侧棱垂直于底面,侧棱长为
的正三角形,侧棱垂直于底面,侧棱长为 ,D为棱
,D为棱 的中点。
的中点。
 平面
平面 ;
;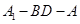 的大小.
的大小.