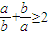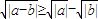题目内容
设a•b>0,则以下不等式中不恒成立的是( )
A、
| ||||||
B、
| ||||||
| C、a2+b2+2≥2a+2b | ||||||
| D、a3+b3≥ab2+a2b |
分析:可用不等式的性质逐个验证,A用到均值不等式,做题时要注意不等式成立需具备的三个条件是否具备.B用到绝对值不等式的性质,C用到均值不等式,注意先变形.D可举反例说明不成立.
解答:解:∵a•b>0∴a,b同号,∴
均为正值,用均值不等式,可得
+
≥2,A成立.
∵应用绝对值不等式的性质,可得
≥
-
,∴B成立.
a2+b2+2=a2+1+b2+1,再分别用均值不等式,可得a2+b2+2≥2a+2b,∴C成立;
当a=-1,b=-2时,a3+b3=-1-8=-9,ab2+a2b=-4-2=-6,a3+b3<ab2+a2b,∴D不恒成立;
故选D
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
∵应用绝对值不等式的性质,可得
| |a-b| |
| |a| |
| |b| |
a2+b2+2=a2+1+b2+1,再分别用均值不等式,可得a2+b2+2≥2a+2b,∴C成立;
当a=-1,b=-2时,a3+b3=-1-8=-9,ab2+a2b=-4-2=-6,a3+b3<ab2+a2b,∴D不恒成立;
故选D
点评:本题考查了不等式的性质,做题时要分清用到的是哪一条性质.

练习册系列答案
相关题目
设a>0,b>0,则以下不等式中不一定成立的是( )
A、
| ||||
| B、ln(ab+1)>0 | ||||
| C、a2+b2+2≥2a+2b | ||||
| D、a3+b3≥2ab2 |