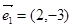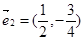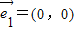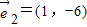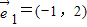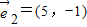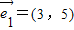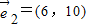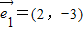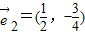题目内容
在下列向量组中,能作为表示它们所在平面内所有向量的基底的是( )
| A、=(0,0)2=(1,-6) |
| B、1=(-1,2)2=(5,-1) |
| C、=(3,5)2=(6,10) |
| D、=(2,-3)2=(,-) |
分析:分别判断四个答案中的一组向量,若它们共线(平行)则他们不能作为表示它们所在平面内所有向量的基底;若他们不共线(平行),故可以作为表示它们所在平面内所有向量的基底.
解答:解:A中,∵
=(0,0)=
,故不适合做为向量的基底;
B中,
1=(-1,2),
2=(5,-1),-1×(-1)-2×5≠0,故两个向量不共线(平行),故可以作为表示它们所在平面内所有向量的基底;
C中,
=(3,5),
2=(6,10),3×10-5×6=0,故两个向量共线(平行),故可以不能作为表示它们所在平面内所有向量的基底;
D中,
=(2,-3)2=(,-),2×(
-)-(-3)×
=0,故两个向量共线(平行),故可以不能作为表示它们所在平面内所有向量的基底;
故选B
点评:本题考查的知识点是平面向量的基本定理及其意义,其中熟练掌握基底的定义--平面内两个不共线的向量,是解答本题的关键.
 涓€棰樹竴棰樻壘绛旀瑙f瀽澶參浜�
涓€棰樹竴棰樻壘绛旀瑙f瀽澶參浜�
涓嬭浇浣滀笟绮剧伒鐩存帴鏌ョ湅鏁翠功绛旀瑙f瀽绔嬪嵆涓嬭浇
练习册系列答案
相关题目


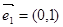
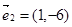 B.
B.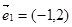

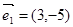
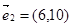 D.
D.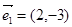
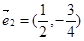
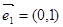
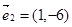 B.
B.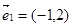
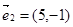
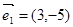
 D.
D.