题目内容
曲线y=ln(2x-1)上的点到直线2x-y+8=0的最短距离是________.

分析:对曲线y=ln(2x-1)进行求导,令y′=2,解出这个点,再根据点到直线的距离进行求解;
解答:∵曲线y=ln(2x-1),
∴y′=
 ,分析知直线2x-y+8=0与曲线y=ln(2x-1)相切的点到直线2x-y+8=0的距离最短,
,分析知直线2x-y+8=0与曲线y=ln(2x-1)相切的点到直线2x-y+8=0的距离最短,y′═
 =2,解得x=1,把x=1代入y=ln(2x-1),
=2,解得x=1,把x=1代入y=ln(2x-1),∴y=0,∴点(1,0)到直线2x-y+8=0的距离最短,
∴d=
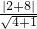 =
=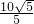 =2
=2 ,
,故答案为2
 .
.点评:此题主要利用导数研究曲线上某点的切线方程,还考查点到直线的距离,此题是一道基础题;

练习册系列答案
相关题目
曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
A、
| ||
B、2
| ||
C、3
| ||
| D、0 |
设点P在曲线y=
ex+1上,点Q在曲线y=ln(2x-2)上,则|PQ|最小值为( )
| 1 |
| 2 |
| A、1-ln2 | ||
B、
| ||
| C、1+ln2 | ||
D、
|