题目内容
极坐标系下曲线 表示圆,则点
表示圆,则点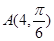 到圆心的距离为 .
到圆心的距离为 .
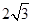
解析试题分析:点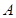 对应的直角坐标为:
对应的直角坐标为: ,
,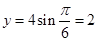 ,所以点
,所以点 .因为
.因为 ,所以
,所以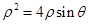 ,即
,即 ,圆的标准方程为:
,圆的标准方程为: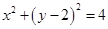 ,圆心
,圆心 ,点到圆心的距离为:
,点到圆心的距离为: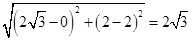 .
.
考点:极坐标与参数方程

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
题目内容
极坐标系下曲线 表示圆,则点
表示圆,则点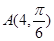 到圆心的距离为 .
到圆心的距离为 .
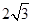
解析试题分析:点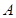 对应的直角坐标为:
对应的直角坐标为: ,
,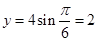 ,所以点
,所以点 .因为
.因为 ,所以
,所以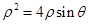 ,即
,即 ,圆的标准方程为:
,圆的标准方程为: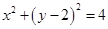 ,圆心
,圆心 ,点到圆心的距离为:
,点到圆心的距离为: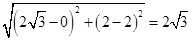 .
.
考点:极坐标与参数方程

 一线名师权威作业本系列答案
一线名师权威作业本系列答案