题目内容
某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同.为保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
【答案】分析:设2001年末汽车保有量为b1万辆,以后各年末汽车保有量依次为b2万辆,b3万辆,,每年新增汽车x万辆,依题意可知b1=30,根据题意可表示出关于bn的递推式,利用等比数列的求和公式求得bn+1,判断出数列的单调性,然后利用数列的极限求得问题的答案.
解答:解:设2001年末汽车保有量为b1万辆,以后各年末汽车保有量依次为b2万辆,b3万辆,,每年新增汽车x万辆,则b1=30,
对于n>1,有
bn+1=bn×0.94+x
=bn-1×0.942+(1+0.94)x
所以bn+1=b1×0.94n+x(1+0.94+0.942+…+0.94n)
=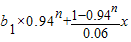 =
=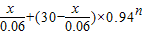
当 ,即x≤1.8时bn+1≤bn≤≤b1=30.
,即x≤1.8时bn+1≤bn≤≤b1=30.
当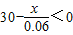 ,即x>1.8时
,即x>1.8时
数列{bn}逐项增加,
可以任意靠近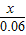
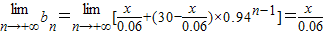
因此,如果要求汽车保有量不超过60万辆,即bn≤60(n=1,2,3,)
则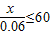 ,即x≤3.6万辆
,即x≤3.6万辆
综上,每年新增汽车不应超过3.6万辆.
点评:本题主要考查了数列的应用,以及数列与不等式的综合.考查了学生综合分析问题和解决问题的能力.
解答:解:设2001年末汽车保有量为b1万辆,以后各年末汽车保有量依次为b2万辆,b3万辆,,每年新增汽车x万辆,则b1=30,
对于n>1,有
bn+1=bn×0.94+x
=bn-1×0.942+(1+0.94)x
所以bn+1=b1×0.94n+x(1+0.94+0.942+…+0.94n)
=
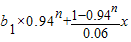 =
=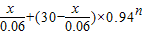
当
 ,即x≤1.8时bn+1≤bn≤≤b1=30.
,即x≤1.8时bn+1≤bn≤≤b1=30.当
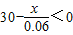 ,即x>1.8时
,即x>1.8时数列{bn}逐项增加,
可以任意靠近
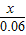
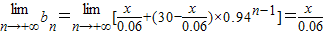
因此,如果要求汽车保有量不超过60万辆,即bn≤60(n=1,2,3,)
则
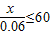 ,即x≤3.6万辆
,即x≤3.6万辆综上,每年新增汽车不应超过3.6万辆.
点评:本题主要考查了数列的应用,以及数列与不等式的综合.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目