题目内容
已知Sn是等比数列的前n项和，Sn=3n+a，则a1=（ ）（选择最佳答案）
分析：由an=sn-sn-1，求出数列的前三项，再由等比数列的定义和性质可得 a22=a1•a3，求出a的值，从而求得a1的值．
解答：解：∵Sn是等比数列的前n项和，Sn=3n+a，则 a1=3+a．
∴a2=s2-s1=9+a-（3+a）=6，a3=s3-s2=27+a-（9+a）=18．
由 a22=a1•a3，可得 36=（3+a）×18，解得 a=-1，
∴a1=3-1=2，
故选C．
∴a2=s2-s1=9+a-（3+a）=6，a3=s3-s2=27+a-（9+a）=18．
由 a22=a1•a3，可得 36=（3+a）×18，解得 a=-1，
∴a1=3-1=2，
故选C．
点评：本题主要考查等比数列的定义和性质，数列的第n项与前n项和之间的关系，属于中档题．
练习册系列答案
相关题目
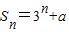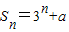，则a1=（ ）（选择最佳答案）
，则a1=（ ）（选择最佳答案）
，则a1=（ ）（选择最佳答案）