题目内容
已知命题p:“直线y=kx+1椭圆
+
=1恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
| x2 |
| 5 |
| y2 |
| a |
∵直线y=kx+1恒过定点A(0,1)
要使得直线y=kx+1与椭圆
+
=1恒有公共点
则只要点A在椭圆
+
=1内或椭圆上即可
方程
+
=1表示椭圆可得a>0且a≠5
∴
解可得a≥1且a≠5
P:a≥1且a≠5
只有一个实数x满足不等式x2+2ax+2a≤0,则可得△=4a2-8a=0
解可得a=0或a=2
∴q:a=0或a=2
由命题“p或q”是假命题可得p,q都为假命题
∴
∴a<0或0<a<1 或a=5.
要使得直线y=kx+1与椭圆
| x2 |
| 5 |
| y2 |
| a |
则只要点A在椭圆
| x2 |
| 5 |
| y2 |
| a |
方程
| x2 |
| 5 |
| y2 |
| a |
∴
|
P:a≥1且a≠5
只有一个实数x满足不等式x2+2ax+2a≤0,则可得△=4a2-8a=0
解可得a=0或a=2
∴q:a=0或a=2
由命题“p或q”是假命题可得p,q都为假命题
∴
|
∴a<0或0<a<1 或a=5.

练习册系列答案
相关题目
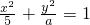 恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.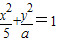 恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.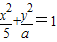 恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.