题目内容
已知命题p:“直线y=kx+1椭圆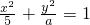 恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
解:∵直线y=kx+1恒过定点A(0,1)
要使得直线y=kx+1与椭圆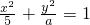 恒有公共点
恒有公共点
则只要点A在椭圆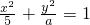 内或椭圆上即可
内或椭圆上即可
方程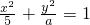 表示椭圆可得a>0且a≠5
表示椭圆可得a>0且a≠5
∴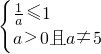 解可得a≥1且a≠5
解可得a≥1且a≠5
P:a≥1且a≠5
只有一个实数x满足不等式x2+2ax+2a≤0,则可得△=4a2-8a=0
解可得a=0或a=2
∴q:a=0或a=2
由命题“p或q”是假命题可得p,q都为假命题
∴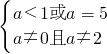
∴a<0或0<a<1 或a=5.
分析:由直线y=kx+1恒过定点A(0,1),要使得直线y=kx+1与椭圆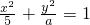 恒有公共点,则只要点A在椭圆
恒有公共点,则只要点A在椭圆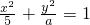 内或椭圆上即可,从而可求P
内或椭圆上即可,从而可求P
若只有一个实数x满足不等式x2+2ax+2a≤0,则可得△=4a2-8a=0,可求q;由命题“p或q”是假命题可得p,q都为假命题
从而可求a得范围
点评:本题主要考查了p或q型复合命题的真假判断的应用,解题的关键还是要能准确的求出命题P,命题q分别为真的范围,注意到命题p中的技巧,而对a>且a≠5的考虑是解题中容易漏掉的地方.
要使得直线y=kx+1与椭圆
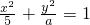 恒有公共点
恒有公共点则只要点A在椭圆
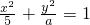 内或椭圆上即可
内或椭圆上即可方程
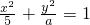 表示椭圆可得a>0且a≠5
表示椭圆可得a>0且a≠5∴
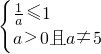 解可得a≥1且a≠5
解可得a≥1且a≠5P:a≥1且a≠5
只有一个实数x满足不等式x2+2ax+2a≤0,则可得△=4a2-8a=0
解可得a=0或a=2
∴q:a=0或a=2
由命题“p或q”是假命题可得p,q都为假命题
∴
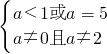
∴a<0或0<a<1 或a=5.
分析:由直线y=kx+1恒过定点A(0,1),要使得直线y=kx+1与椭圆
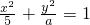 恒有公共点,则只要点A在椭圆
恒有公共点,则只要点A在椭圆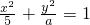 内或椭圆上即可,从而可求P
内或椭圆上即可,从而可求P若只有一个实数x满足不等式x2+2ax+2a≤0,则可得△=4a2-8a=0,可求q;由命题“p或q”是假命题可得p,q都为假命题
从而可求a得范围
点评:本题主要考查了p或q型复合命题的真假判断的应用,解题的关键还是要能准确的求出命题P,命题q分别为真的范围,注意到命题p中的技巧,而对a>且a≠5的考虑是解题中容易漏掉的地方.

练习册系列答案
相关题目
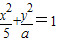 恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.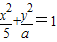 恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.
恒有公共点”命题q:只有一个实数x满足不等式x2+2ax+2a≤0.若命题“p或q”是假命题,求实数a的取值范围.