题目内容
已知三角形的三边长分别为a、b、
,则三角形的最大内角是( )
| a2+ab+b2 |
分析:利用三角形中大边对大角可得,三角形的最大内角是
所对的角,设为θ,由余弦定理求得
cosθ 的值,可得θ的值.
| a2+ab+b2 |
cosθ 的值,可得θ的值.
解答:解:∵三角形的三边长分别为a、b、
中,
为最大边,
则三角形的最大内角是
所对的角,设为θ.
由余弦定理可得 cosθ=
=-
,∴θ=120°,
故选B.
| a2+ab+b2 |
| a2+ab+b2 |
则三角形的最大内角是
| a2+ab+b2 |
由余弦定理可得 cosθ=
| a2+b 2 - (a 2+ab+b 2) |
| 2ab |
| 1 |
| 2 |
故选B.
点评:本题主要考查余弦定理的应用,以及大边对大角,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
已知三角形的三边长分别是
2m+3, ,
, 且m>0,则这个三角形的最大角为
且m>0,则这个三角形的最大角为
[
]|
A .150° |
B .135° |
|
C .120° |
D .90° |
 ,
, 且m>0,则这个三角形的最大角为
且m>0,则这个三角形的最大角为 的三边长
的三边长 ,满足
,满足
 均为正整数,且
均为正整数,且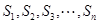 ,且
,且 ,求满足不等式
,求满足不等式 的所有
的所有 的值;
的值; 满足
满足 ,证明数列
,证明数列 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且 是正整数.
是正整数.