题目内容
12. 已知如图所示的非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,请分别作出满足下列条件的向量$\overrightarrow{c}$.
已知如图所示的非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,请分别作出满足下列条件的向量$\overrightarrow{c}$.(1)$\overrightarrow{c}$=2$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$;
(2)$\overrightarrow{c}$=$\frac{1}{2}$$\overrightarrow{a}$-2$\overrightarrow{b}$.
分析 直接运用向量加法的三角形法则,减法的三角形法则画图.
解答 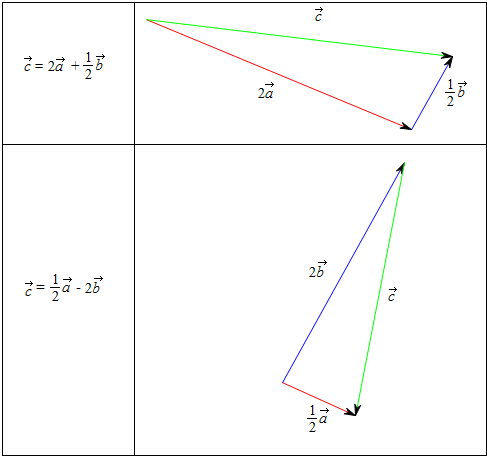 (1)$\overrightarrow{c}$=2$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$,画图过程如下:
(1)$\overrightarrow{c}$=2$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$,画图过程如下:
将$\overrightarrow{a}$伸长一倍(红线),
将$\overrightarrow{b}$缩短到一半(蓝线),
根据向量加法的“三角形法则”,
将它们首尾相连,
得到绿线,就是$\overrightarrow{c}$;
(2)$\overrightarrow{c}$=$\frac{1}{2}$$\overrightarrow{a}$-2$\overrightarrow{b}$,画图过程如下:
将$\overrightarrow{a}$缩短到一半(红线),
将$\overrightarrow{b}$伸长一倍(蓝线),
根据向量减法的“三角形法则”,
将它们起点重合,
连接两向量的终点,
得到绿线,就是$\overrightarrow{c}$;
点评 本题主要考查了向量加法的三角形法则和减法的三角形法则,运用几何图形表示向量的运算,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目