题目内容
已知a,b是两条不重合的直线,α,β是两个不同的平面,则下列命题正确的是( )
分析:由线面垂直,面面垂直的几何特征,及线面关系的几何特征可判断A;由面面平行的判定定理,可判断B;由线面平行,面面平行的几何特征,可判断C;由线面垂直及面面平行的几何特征可判断D.
解答:解:若a⊥α,β⊥α,则a∥β或a?β,故A不正确;
若a,b?α,a∥β,b∥β,则当a,b相交时,α∥β;a∥b时,α∥β不一定成立,故B不正确;
若a∥b,b∥α,则a∥α或a?α,故C不正确;
若a⊥α,α∥β,则由两个平行平面中一个与直线垂直,另外一个也必与该直线垂直得到a⊥β,故D正确
故选D
若a,b?α,a∥β,b∥β,则当a,b相交时,α∥β;a∥b时,α∥β不一定成立,故B不正确;
若a∥b,b∥α,则a∥α或a?α,故C不正确;
若a⊥α,α∥β,则由两个平行平面中一个与直线垂直,另外一个也必与该直线垂直得到a⊥β,故D正确
故选D
点评:本题考查的知识点是空间中直线与平面之间的位置关系,空间中直线与直线之间的位置关系,平面与平面之间的位置关系,其中熟练掌握空间线面关系的几何特征,判定,性质是解答的关键.

练习册系列答案
相关题目
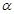 ,
,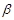 是两个不重合的平面,下列命题中正确的是( )
是两个不重合的平面,下列命题中正确的是( )
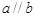 ,
,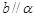 ,则
,则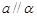
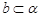 ,
,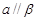 ,
,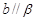 ,则
,则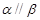
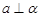 ,
,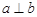
 ,且
,且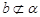 时,若
时,若 ∥
∥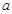 ∥
∥