题目内容
(本题满分12分)
已知顶点在坐标原点,焦点在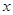 轴上的抛物线被直线
轴上的抛物线被直线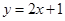 截得的弦长为
截得的弦长为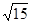 ,求抛物线的方程。
,求抛物线的方程。
【答案】

【解析】由于抛物线的焦点在x轴上,可设抛物线方程为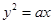 m
m
然后与抛物线方程联立,消去y后得关于x的一元二次方程,利用弦长公式可建立关于a 的方程,求出a的值.
解:设抛物线的方程为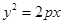 ,则
,则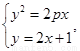 消去
消去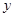 得
得
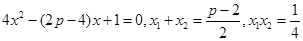
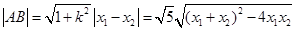
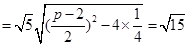 ,
,
则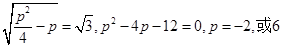


练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面