题目内容
已知数列 满足
满足 =-1,
=-1, ,数列
,数列 满足
满足
(1)求证:数列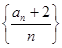 为等比数列,并求数列
为等比数列,并求数列 的通项公式.
的通项公式.
(2)求证:当 时,
时,
(3)设数列 的前
的前 项和为
项和为 ,求证:当
,求证:当 时,
时, .
.
【答案】
(1)见解析(2)见解析(3)见解析
【解析】(1)由题目条件可知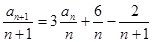 ,即
,即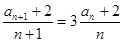 ,问题
,问题
得证.
(2)本小题易采用数学归纳法进行证明:(1)先验证:当n=2时,是否成立,
(2)假设n=k时,命题成立,再证明n=k+1时,命题也成立,在证明过程
中必须要用上n=k时的归纳假设否则证明无效.
解:(1)由题意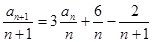 ,即
,即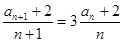
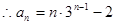 ………………………………4分
………………………………4分
(2)当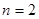 时,
时,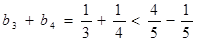 即
即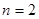 时命题成立
时命题成立
假设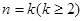 时命题成立,即
时命题成立,即
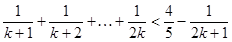
当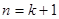 时,
时,
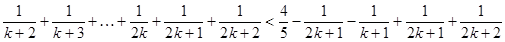
=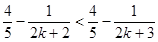 即
即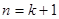 时命题也成立
时命题也成立
综上,对于任意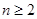 ,
,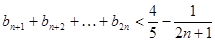 ………………8分
………………8分
(2)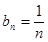 当
当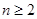 时,
时,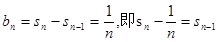
平方则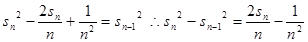
叠加得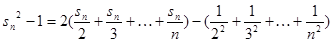
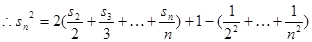
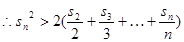 ……………………………………13分
……………………………………13分
【解析】(1)由题目条件可知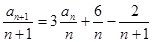 ,即
,即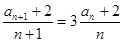 ,问题
,问题
得证.
(2)本小题易采用数学归纳法进行证明:(1)先验证:当n=2时,是否成立,
(2)假设n=k时,命题成立,再证明n=k+1时,命题也成立,在证明过程
中必须要用上n=k时的归纳假设否则证明无效.

练习册系列答案
相关题目
 满足
满足
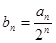 ,求数列
,求数列 的前
的前 项和
项和 .
. 满足
满足
 ,求数列
,求数列 的前
的前 项和
项和 .
. 满足
满足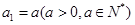 ,
,
 .
. ;
; ,若将
,若将 按从小到大的顺序排列后,此三项均能构成等
按从小到大的顺序排列后,此三项均能构成等 .①求
.①求 的值及对应的数列
的值及对应的数列 .
. 为数列
为数列 ,使得
,使得 对任意正整数
对任意正整数 满足
满足 ,(1)若
,(1)若 ,求
,求 ;
; ,使当
,使当 时,
时, ,否则说明理由;
,否则说明理由; ,求
,求 项的和
项的和 (用
(用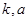 表示)
表示)