题目内容
求下列函数单调区间和极值,y=f(x)=x3-
x2-2x+5.
| 1 | 2 |
分析:先求出其导函数,利用导函数值的正负对应的区间即可求出原函数的单调区间,进而求出极值.
解答:解:∵y=f(x)=x3-
x2-2x+5
∴y′=3x2-x-2=(x-1)(3x+2)
令y′>0,可得x<-
或x>1;令y′<0,可得-
<x<1,
∴函数的单调递增区间为(-∞,-
)和(1,+∞);单调减区间为(-
,1)
当x=-
时,函数取得极大值
;当x=1时,函数取得极小值
| 1 |
| 2 |
∴y′=3x2-x-2=(x-1)(3x+2)
令y′>0,可得x<-
| 2 |
| 3 |
| 2 |
| 3 |
∴函数的单调递增区间为(-∞,-
| 2 |
| 3 |
| 2 |
| 3 |
当x=-
| 2 |
| 3 |
| 27 |
| 49 |
| 7 |
| 2 |
点评:本题主要考查函数与导数的综合应用能力,具体涉及到用导数来研究函数的单调性、极值,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
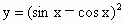 .
.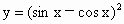 .
.
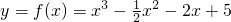 .
.