题目内容
抛物线D以双曲线C:8y2-8x2=1的焦点F(0,c),(c>0)为焦点.
(1)求抛物线D的标准方程;
(2)过直线l:y=x-1上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;
(3)在(2)的条件下,若直线PQ交抛物线D于M,N两点,求证:|PM|·|QN|=|QM|·|PN|
答案:
解析:
解析:
|
解:(1)由题意, 所以 (2)设 由 抛物线D在点A处的切线方程为 而A点处的切线过点 即 同理, 可见,点A,B在直线 令 所以,直线AB过定点Q(1,1) 6分 (3)设 直线PQ的方程为 由 得 由韦达定理, 而 将 (*)的左边 =0. 因而有|PM|·|QN|=|QM|·|PN|.14分
|

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
设动点P在直线x=1上,O为坐标原点.以OP为直角边、点O为直角顶点作等腰Rt△OPQ,则动点Q的轨迹是
( )
( )
| A、圆 | B、两条平行直线 | C、抛物线 | D、双曲线 |
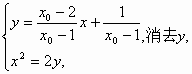
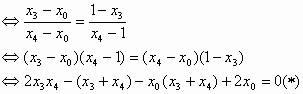 12分
12分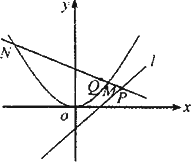
 上的动点,定点D(1,0).点P在DM上,点N在CM上,且满足
上的动点,定点D(1,0).点P在DM上,点N在CM上,且满足 .动点
.动点 的轨迹为(***)
的轨迹为(***)