题目内容
抛物线D以双曲线C:8y2-8x2=1的焦点F(0,c),(c>0)为焦点.(1)求抛物线D的标准方程;
(2)过直线l:y=x-1上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;
(3)在(2)的条件下,若直线PQ交抛物线D于M,N两点,求证:|PM|•|QN|=|QM|•|PN|
【答案】分析:(1)由题意,求出c值,从而得出 ,最后写出抛物线D的标准方程;
,最后写出抛物线D的标准方程;
(2)先设出切点坐标A(x1,y1),B(x2,y2),利用导数的几何意义求以A、B为切点的切线方程,再设出P(x,x-1),代入两条切线方程,得x-1=xx1-y1.x-1=xx2-y2.故直线AB的方程为x-1=xx-y,过定点(1,1)
(3)先写出直线PQ的方程y= (x-1)+1,代入抛物线方程
(x-1)+1,代入抛物线方程  ,得关于x的一元二次方程,为利用韦达定理准备条件,再设M(x3,y3),N(x4,y4),要证
,得关于x的一元二次方程,为利用韦达定理准备条件,再设M(x3,y3),N(x4,y4),要证  =
= ,只需证明
,只需证明  ,即2x3x4-(1+x)(x3+x4)+2x=0,最后利用韦达定理将x3+x4和x3x4代入即可得证.
,即2x3x4-(1+x)(x3+x4)+2x=0,最后利用韦达定理将x3+x4和x3x4代入即可得证.
解答:解:(1)由题意,c2= .
.
所以 ,抛物线D的标准方程为x2=2y.…(3分)
,抛物线D的标准方程为x2=2y.…(3分)
(2)设A(x1,y1),B(x2,y2),P(x,x-1),
由
抛物线D在点A处的切线方程为y-y1=x1(x-x1),即y=x1x-y1.…(4分)
而A点处的切线过点P(x,x-1),所以x-1=x1x-y1,
即(x1-1)x+1-y1=0.
同理,(x2-1)x+1-y2=0.
可见,点A,B在直线(x-1)x+1-y=0上.
令x-1=0,1-y=0,解得x=y=1
所以,直线AB过定点Q(1,1)…(6分)
(3) 设P(x,x-1),M(x3,y3),N(x4,y4),
设P(x,x-1),M(x3,y3),N(x4,y4),
直线PQ的方程为y= .
.
由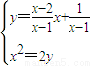 ,消去y,
,消去y,
得x2-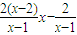 =0.
=0.
由韦达定理,x3+x4= .…(9分)
.…(9分)
而|PM|•|QN|=|QM|•|PN|?

…(12分)
将x3+x4= 代入方程(*)的左边,得
代入方程(*)的左边,得
(*)的左边=-
=
=0.
因而有|PM|•|QN|=|QM|•|PN|.…(14分)
点评:本题考察了抛物线的切线方程,直线与抛物线相交的性质,解题时要特别注意韦达定理在解题时的重要运用,还要有较强的运算推理能力
 ,最后写出抛物线D的标准方程;
,最后写出抛物线D的标准方程;(2)先设出切点坐标A(x1,y1),B(x2,y2),利用导数的几何意义求以A、B为切点的切线方程,再设出P(x,x-1),代入两条切线方程,得x-1=xx1-y1.x-1=xx2-y2.故直线AB的方程为x-1=xx-y,过定点(1,1)
(3)先写出直线PQ的方程y=
 (x-1)+1,代入抛物线方程
(x-1)+1,代入抛物线方程  ,得关于x的一元二次方程,为利用韦达定理准备条件,再设M(x3,y3),N(x4,y4),要证
,得关于x的一元二次方程,为利用韦达定理准备条件,再设M(x3,y3),N(x4,y4),要证  =
= ,只需证明
,只需证明  ,即2x3x4-(1+x)(x3+x4)+2x=0,最后利用韦达定理将x3+x4和x3x4代入即可得证.
,即2x3x4-(1+x)(x3+x4)+2x=0,最后利用韦达定理将x3+x4和x3x4代入即可得证.解答:解:(1)由题意,c2=
 .
.所以
 ,抛物线D的标准方程为x2=2y.…(3分)
,抛物线D的标准方程为x2=2y.…(3分)(2)设A(x1,y1),B(x2,y2),P(x,x-1),
由

抛物线D在点A处的切线方程为y-y1=x1(x-x1),即y=x1x-y1.…(4分)
而A点处的切线过点P(x,x-1),所以x-1=x1x-y1,
即(x1-1)x+1-y1=0.
同理,(x2-1)x+1-y2=0.
可见,点A,B在直线(x-1)x+1-y=0上.
令x-1=0,1-y=0,解得x=y=1
所以,直线AB过定点Q(1,1)…(6分)
(3)
 设P(x,x-1),M(x3,y3),N(x4,y4),
设P(x,x-1),M(x3,y3),N(x4,y4),直线PQ的方程为y=
 .
.由
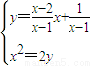 ,消去y,
,消去y,得x2-
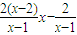 =0.
=0.由韦达定理,x3+x4=
 .…(9分)
.…(9分)而|PM|•|QN|=|QM|•|PN|?


…(12分)
将x3+x4=
 代入方程(*)的左边,得
代入方程(*)的左边,得(*)的左边=-

=

=0.
因而有|PM|•|QN|=|QM|•|PN|.…(14分)
点评:本题考察了抛物线的切线方程,直线与抛物线相交的性质,解题时要特别注意韦达定理在解题时的重要运用,还要有较强的运算推理能力

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
设动点P在直线x=1上,O为坐标原点.以OP为直角边、点O为直角顶点作等腰Rt△OPQ,则动点Q的轨迹是
( )
( )
| A、圆 | B、两条平行直线 | C、抛物线 | D、双曲线 |
 上的动点,定点D(1,0).点P在DM上,点N在CM上,且满足
上的动点,定点D(1,0).点P在DM上,点N在CM上,且满足 .动点
.动点 的轨迹为(***)
的轨迹为(***)