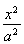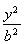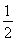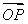题目内容
已知椭圆E:(1)若F2(2,0)关于直线y=![]() x+
x+![]() 的对称点在椭圆E上,求该椭圆E的方程;
的对称点在椭圆E上,求该椭圆E的方程;
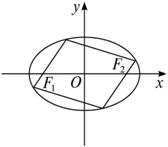
(2)若椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),求这个平行四边形面积的最大值.
解:(1)设F2(2,0)关于y=![]() x+
x+![]() 对称的点为(x0,y0),则
对称的点为(x0,y0),则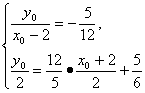
解得x0=-2,y0=![]() .
.
所以将x0=-2,y0=![]()
代入椭圆方程得![]() +
+![]() =1且a2-b2=4.
=1且a2-b2=4.
解得a2=9或a2=![]() (舍去).所以椭圆的方程为
(舍去).所以椭圆的方程为![]() =1.
=1.
(2)设AB:x=my+c,CD:x=my-c.
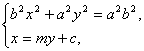
消去x,得(b2m2+a2)y2+2b2mcy-b4=0.
y1+y2=-![]() ,y1y2=-
,y1y2=-![]() ,
,
|AB|=2ab2![]() ,d=
,d=![]() ,
,
![]() =4ab2c
=4ab2c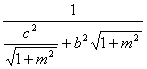 .
.
当![]() ≥1时,
≥1时, ![]() ≤4ab2c·
≤4ab2c·![]() =2ab;
=2ab;
当0<![]() <1时,
<1时, ![]() ≤4ab2c
≤4ab2c![]() =
=![]() .
.

练习册系列答案
相关题目
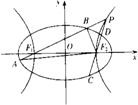 如图,已知椭圆
如图,已知椭圆