题目内容
已知p:?x∈R,2x>m(x2+1),q:?x0∈R,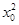 +2x0-m-1=0,且p∧q为真,求实数m的取值范围.
+2x0-m-1=0,且p∧q为真,求实数m的取值范围.
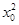 +2x0-m-1=0,且p∧q为真,求实数m的取值范围.
+2x0-m-1=0,且p∧q为真,求实数m的取值范围.-2≤m<-1.
试题分析:2x>m(x2+1) 可化为mx2-2x+m<0.
所以若p:?x∈R, 2x>m(x2+1)为真,
则mx2-2x+m<0对任意的x∈R恒成立.
由此可得m的取值范围.
若q:?x0∈R,
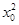 +2x0-m-1=0为真,
+2x0-m-1=0为真,则方程x2+2x-m-1=0有实根,由此可得m的取值范围.
p∧q为真,则p、q 均为真命题,取m的公共部分便得m的取值范围.
试题解析:2x>m(x2+1) 可化为mx2-2x+m<0.
若p:?x∈R, 2x>m(x2+1)为真,
则mx2-2x+m<0对任意的x∈R恒成立.
当m=0时,不等式可化为-2x<0,显然不恒成立;
当m≠0时,有m<0,Δ= 4-4m2<0,∴m<-1.
若q:?x0∈R,
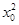 +2x0-m-1=0为真,
+2x0-m-1=0为真,则方程x2+2x-m-1=0有实根,
∴Δ=4+4(m+1)≥0,∴m≥-2.
又p∧q为真,故p、q 均为真命题.
∴m<-1且m≥-2,∴-2≤m<-1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
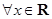 ,
,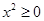 ”的否定为 ( )
”的否定为 ( )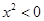
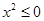
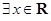 ,
,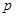 :对任意
:对任意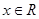 ,有
,有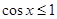 ,则( )
,则( )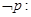 存在
存在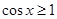
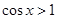
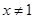 ,则
,则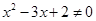 ”的逆否命题是“若
”的逆否命题是“若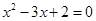 ,则
,则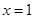 ”
”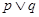 为真命题,则
为真命题,则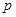 、
、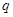 均为真命题
均为真命题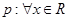 ,
,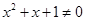 ,则
,则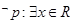 ,
,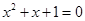
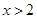 ”是“
”是“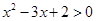 ”的充分不必要条件
”的充分不必要条件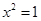 ,则
,则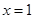 ”的否命题是“若
”的否命题是“若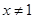 ”;
”;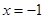 ”是“
”是“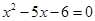 ”的必要不充分条件;
”的必要不充分条件;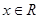 ,使得
,使得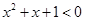 ”的否定是“对任意
”的否定是“对任意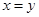 ,则
,则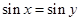 ”的逆否命题为真.
”的逆否命题为真.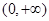 上,函数
上,函数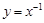 ,
,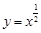 ,
,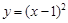 ,
,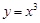 中有三个是增函数;
中有三个是增函数;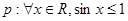 .则
.则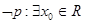 ,使
,使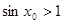 ;
;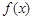 是偶函数,则
是偶函数,则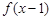 的图象关于直线
的图象关于直线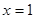 对称;
对称;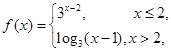 则方程
则方程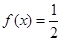 有
有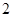 个实数根.
个实数根.
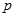 :函数
:函数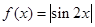 的最小正周期为
的最小正周期为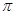 ;命题
;命题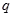 :若函数
:若函数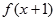 为偶函数,则
为偶函数,则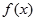 关于
关于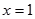 对称.则下列命题是真命题的是( )
对称.则下列命题是真命题的是( )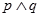
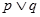
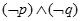
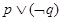
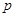 且
且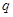 ”为假命题,则
”为假命题,则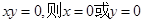 ”的否命题为“若
”的否命题为“若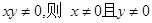 ”
”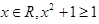 ”的否定是“存在
”的否定是“存在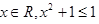 ”
”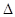 ABC中,“
ABC中,“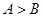 ”是“
”是“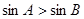 ”的充要条件
”的充要条件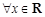 ,
,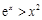 ”的否定是( )
”的否定是( )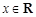 ,使
,使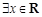 ,使
,使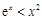
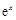 ≤
≤