题目内容
已知椭圆的方程为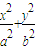 =1(a>b>0),它的一个焦点与抛物线y2=8x的焦点重合,离心率e=
=1(a>b>0),它的一个焦点与抛物线y2=8x的焦点重合,离心率e=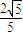 ,过椭圆的右焦点F作与坐标轴不垂直的直线l,交椭圆于A、B两点.
,过椭圆的右焦点F作与坐标轴不垂直的直线l,交椭圆于A、B两点.(1)求椭圆的标准方程;
(2)设点M(1,0),且
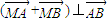 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(1)由椭圆和y2=8x抛物线有共同的焦点,求出抛物线的焦点坐标,离心率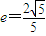 ,根据a2=b2+c2,即可求得椭圆C的方程;
,根据a2=b2+c2,即可求得椭圆C的方程;
(2)设出直线l的方程和点A,B的坐标,并代入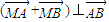 ,联立联立消去y,得到关于x的一元二次方程,△>0,利用韦达定理即可求得.
,联立联立消去y,得到关于x的一元二次方程,△>0,利用韦达定理即可求得.
解答:解:(1)设椭圆的右焦点为(c,0),
因为y2=8x的焦点坐标为(2,0),所以c=2
因为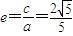 ,则a2=5,b2=1
,则a2=5,b2=1
故椭圆方程为: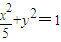
(2)由(I)得F(2,0),
设l的方程为y=k(x-2)(k≠0)
代入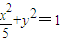 ,得(5k2+1)x2-20k2x+20k2-5=0,
,得(5k2+1)x2-20k2x+20k2-5=0,
设A(x1,y1),B(x2,y2),
则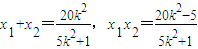 ,
,
∴y1+y2=k(x1+x2-4),y1-y2=k(x1-x2)
∴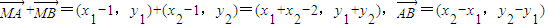
∵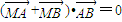 ,∴(x1+x2-2)(x2-x1)+(y2-y1)(y1+y2)=0∴
,∴(x1+x2-2)(x2-x1)+(y2-y1)(y1+y2)=0∴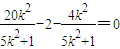 ,
,
∴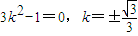
所以直线l的方程为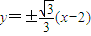 .
.
点评:此题是个难题.考查抛物线的定义和简单的几何性质,待定系数法求椭圆的标准方程,以及直线和椭圆相交中的有关中点弦的问题,综合性强,特别是问题(2)的设问形式,增加了题目的难度,注意直线与圆锥曲线相交,△>0.体现了数形结合和转化的思想方法.
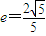 ,根据a2=b2+c2,即可求得椭圆C的方程;
,根据a2=b2+c2,即可求得椭圆C的方程;(2)设出直线l的方程和点A,B的坐标,并代入
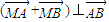 ,联立联立消去y,得到关于x的一元二次方程,△>0,利用韦达定理即可求得.
,联立联立消去y,得到关于x的一元二次方程,△>0,利用韦达定理即可求得.解答:解:(1)设椭圆的右焦点为(c,0),
因为y2=8x的焦点坐标为(2,0),所以c=2
因为
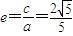 ,则a2=5,b2=1
,则a2=5,b2=1故椭圆方程为:
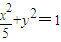
(2)由(I)得F(2,0),
设l的方程为y=k(x-2)(k≠0)
代入
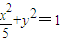 ,得(5k2+1)x2-20k2x+20k2-5=0,
,得(5k2+1)x2-20k2x+20k2-5=0,设A(x1,y1),B(x2,y2),
则
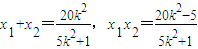 ,
,∴y1+y2=k(x1+x2-4),y1-y2=k(x1-x2)
∴
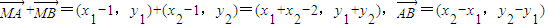
∵
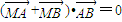 ,∴(x1+x2-2)(x2-x1)+(y2-y1)(y1+y2)=0∴
,∴(x1+x2-2)(x2-x1)+(y2-y1)(y1+y2)=0∴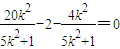 ,
,∴
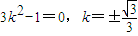
所以直线l的方程为
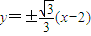 .
.点评:此题是个难题.考查抛物线的定义和简单的几何性质,待定系数法求椭圆的标准方程,以及直线和椭圆相交中的有关中点弦的问题,综合性强,特别是问题(2)的设问形式,增加了题目的难度,注意直线与圆锥曲线相交,△>0.体现了数形结合和转化的思想方法.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目