题目内容
已知椭圆的方程为(1)若![]() 与a=(-3,1)共线,求椭圆的方程;
与a=(-3,1)共线,求椭圆的方程;
(2)若在左准线上存在点R,使△PQR为正三角形,求椭圆的离心率e.
(文)已知函数f(x)=2x(x>0),g(x)=![]() .
.
(1)求F(x)=2f(x)+[g(x)]2的最小值;
(2)在x轴正半轴上有一动点C(x,0),过C作x轴的垂线分别与f(x)、g(x)的图象交于点A、B,试将△AOC与△BOC的面积的平方差表示为x的函数h(x),并判断h(x)是否存在极值,若存在,求出极值;若不存在,请说明理由.
答案:解:(1)将直线PQ的方程y=x+1,代入![]() +
+![]() =1并化简,得(a2+b2)x2+2a2x+a2-a2b2=0.
=1并化简,得(a2+b2)x2+2a2x+a2-a2b2=0.
令P(x1,y1),Q(x2,y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
由![]() =(x1+x2,y1+y2),
=(x1+x2,y1+y2),![]() 与a=(-3,1)共线,得3(y1+y2)+(x1+x2)=0.
与a=(-3,1)共线,得3(y1+y2)+(x1+x2)=0.
∴3(x1+x2+2)+(x1+x2)=0.∴x1+x2=-![]() ,即
,即![]() =-
=-![]() .∴a2=3b2.
.∴a2=3b2.
又a2=b2+1,∴a2=![]() ,b2=
,b2=![]() .∴椭圆的方程为
.∴椭圆的方程为![]() +2y2=1.
+2y2=1.
(2)如图,设线段PQ的中点为M.
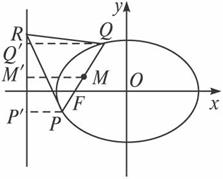
过点P、M、Q分别作准线的垂线,垂足分别为P′、M′、Q′,则|MM′|=![]() (|PP′|+|QQ′|)
(|PP′|+|QQ′|)
=![]() .∵∠QFX=
.∵∠QFX=![]() ,∴∠FMM′=
,∴∠FMM′=![]() .∴∠M′MR=
.∴∠M′MR=![]() .∴|RM|=
.∴|RM|=![]() |MM′|.又|RM|=
|MM′|.又|RM|=![]() |PQ|,∴
|PQ|,∴![]() |PQ|.∴e=
|PQ|.∴e=![]() .
.
(文)解:(1)F(x)=2x+![]() ≥2
≥2![]() ,当且仅当2x=
,当且仅当2x=![]() ,即x=
,即x=![]() 时取等号.
时取等号.
(2)△AOC与△BOC的面积分别为![]() x2、
x2、![]() ,所以h(x)=
,所以h(x)=![]() (2x4-x),h′(x)=
(2x4-x),h′(x)=![]() (8x3-1).
(8x3-1).
当0<x<![]() 时,h′(x)<0,h(x)在(0,
时,h′(x)<0,h(x)在(0,![]() )上单调递减;当x>
)上单调递减;当x>![]() 时,h′(x)>0,h(x)在(
时,h′(x)>0,h(x)在(![]() ,+∞)上单调递增,且h(x)在(0,+∞)上连续,所以h(x)在x=
,+∞)上单调递增,且h(x)在(0,+∞)上连续,所以h(x)在x=![]() 处有极小值h(
处有极小值h(![]() )=
)=![]() .
.
