题目内容
已知函数f(x)=ax3+bsin x+4(a,b∈R),f(lg(log210))=5,则f(lg(lg 2))等于 ( ).
| A.-5 | B.-1 |
| C.3 | D.4 |
C
解析

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
定义在R上的偶函数f(x)在(0,+∞)上是增函数,且f( )=0,则不等式
)=0,则不等式 的解集是( )
的解集是( )
A.(0, ) ) | B.( ,+∞) ,+∞) |
C.(- ,0)∪( ,0)∪( ,+∞) ,+∞) | D.(-∞,- )∪(0, )∪(0, ) ) |
若不等式x2+ax+1≥0对于一切x∈(0, ]恒成立,则a的最小值是( )
]恒成立,则a的最小值是( )
| A.0 | B.2 | C.- | D.-3 |
下列函数中,不满足f(2x)=2f(x)的是( ).
| A.f(x)=|x| | B.f(x)=x-|x| | C.f(x)=x+1 | D.f(x)=-x |
下列函数中,在区间(0,+∞)上为增函数的是 ( ).
| A.y=lg(x+2) | B.y=- |
C.y= x x | D.y=x+ |
f(x)= 则下列关于y=f[f(x)]-2的零点个数判断正确( ).
则下列关于y=f[f(x)]-2的零点个数判断正确( ).
| A.当k=0时,有无数个零点, |
| B.当k<0时,有3个零点 |
| C.当k>0时,有3个零点 |
| D.无论k取何值,都有4个零点 |
若奇函数f(x)在(0,+∞)上的解析式是f(x)=x(1-x),则在(-∞,0)上,f(x)的解析式是( ).
| A.f(x)=-x(1-x) | B.f(x)=x(1+x) |
| C.f(x)=-x(1+x) | D.f(x)=x(1-x) |
 的正方体
的正方体 的对角线
的对角线 上任取一点
上任取一点 ,以
,以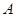 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数
