题目内容
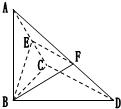如图，已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且| AE |
| AC |
| AF |
| AD |
| 6 |
| 7 |
| 6 |
| 7 |
分析：根据平行线分线段成比例定理，可得EF∥CD，进而可得EF⊥平面ABC，再由面面垂直的判定定理得到平面BEF⊥平面ABC，由面面垂直的性质定理可得BE⊥平面ACD，则BE⊥AC．故只须让所求λ的值能证明BE⊥AC即可．解三角形△ABC中可求出λ的值．
解答：解：∵AB⊥平面BCD，∴AB⊥CD，
∵CD⊥BC且AB∩BC=B，∴CD⊥平面ABC
又∵
=
=λ（0＜λ＜1），
∴不论λ为何值，恒有EF∥CD，
∴EF⊥平面ABC，BE?平面ABC，
∴BE⊥EF，
又平面BEF⊥平面ACD，
∴BE⊥平面ACD，∴BE⊥AC
∵BC=CD=1，∠BCD=90°，∠ADB=60°，
∴BD=
，AB=
tan60°=
∴AC=
，
由AB2=AE•AC得AE=
故当λ=
=
时，平面BEF⊥平面ACD
故答案为：
∵CD⊥BC且AB∩BC=B，∴CD⊥平面ABC
又∵
| AE |
| AC |
| AF |
| AD |
∴不论λ为何值，恒有EF∥CD，
∴EF⊥平面ABC，BE?平面ABC，
∴BE⊥EF，
又平面BEF⊥平面ACD，
∴BE⊥平面ACD，∴BE⊥AC
∵BC=CD=1，∠BCD=90°，∠ADB=60°，
∴BD=
| 2 |
| 2 |
| 6 |
∴AC=
| 7 |
由AB2=AE•AC得AE=
| 6 | ||
|
故当λ=
| AE |
| AC |
| 6 |
| 7 |
故答案为：
| 6 |
| 7 |
点评：本题考查了面面垂直的判定．在证明面面垂直时，其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直．
练习册系列答案
相关题目
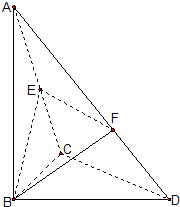如图，已知△BCD中，∠BCD=90°，AB⊥平面BCD，
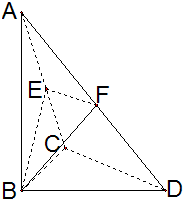如图，已知△BCD中，∠BCD=90°，AB⊥平面BCD，BC=CD=1，
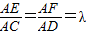（0＜λ＜1）．若平面BEF⊥平面ACD，则λ的值为 ．
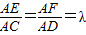（0＜λ＜1）．若平面BEF⊥平面ACD，则λ的值为 ．