题目内容
5.已知函数|x2+3x|-a|x-1|=0有四个不同的实数根,求a的取值范围.分析 由题意可知函数f(x)=|x2+3x|与g(x)=a|x-1|有四个不同的交点,作函数的图象,并找出临界值,结合图象求范围即可.
解答 解:∵方程|x2+3x|-a|x-1|=0有四个不同的实数根,
∴函数f(x)=|x2+3x|与g(x)=a|x-1|有四个不同的交点,
作函数f(x)=|x2+3x|与g(x)=a|x-1|的图象如下,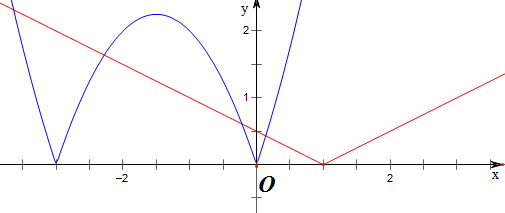
当-3<x<0时,
f(x)=|x2+3x|=-(x2+3x),f′(x)=-2x-3;
g(x)=a|x-1|=-ax+a;
设g(x)与f(x)相切于点A(b,f(b)),
则$\frac{f(b)-0}{b-1}$=-2b-3;
解得,b=-1或b=3(舍去);
故-a=f′(-1)=2-3=-1;
故a=1;
结合图象知,0<a<1.
点评 本题考查了方程的根与函数的图象的关系应用,同时考查了导数的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
 如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )
如图,一条直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,F为抛物线的焦点,若△ABO与△AFO面积之和的最小值为50$\sqrt{5}$,则抛物线的方程为( )| A. | y2=20x | B. | y2=10x | C. | y2=5x | D. | y2=$\frac{5}{2}$x |
10.已知全集U={1,2,3,4,5},集合M={3,4,5},N={1,2,5},则集合{1,2}可以表示为( )
| A. | M∩N | B. | (∁UM)∩N | C. | M∩(∁UN) | D. | (∁UM)∩(∁UN) |
17.已知平行四边形OABC,$\overrightarrow{OA}$=(4,2),$\overrightarrow{OC}$=(2,6),则$\overrightarrow{OB}$与$\overrightarrow{AC}$夹角的余弦是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
14.已知实数a,b,c满足不等式0<a<b<c<1,且M=2a,N=5-b,P=($\frac{1}{7}$)c,则M、N、P的大小关系为( )
| A. | M>N>P | B. | P<M<N | C. | N>P>M |
 的图象是( )
的图象是( )
 为平面向量,若
为平面向量,若 与
与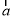 的夹角为
的夹角为 与
与 的夹角为
的夹角为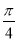 ,则
,则 ( )
( )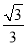 B.
B.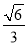
 D.2
D.2