题目内容
已知椭圆与双曲线
有相同的焦点，且椭圆过点
，
（1）求椭圆方程；
（2）直线
过点
交椭圆于
两点，且
，求直线的方程。
；
解析:
①依题意得，双曲线方程为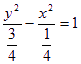
∴双曲线两焦点为（0，-1），（0，1）
设所求椭圆方程为
∴
又∵点
在椭圆上
∴
整理得
解得
，∴
∴椭圆方程为
②依题意得M为AB中点，设
直线方程为
，则
由
，得
整理得
∵点A、B互异
∴
解得 
直线方程为
即
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
与双曲线
有相同的焦点，则椭圆的离心率为
B． 
C． 
D．
与双曲线
有相同的焦点
和
，若
是
的等比中项，
是
与
的等差中项，则椭圆的离心率是（ ）
B．
C．
D．
与双曲线
有相同的焦点
和
，若c是a与m的等比中项，n2是2m2与c2的等差中项，则椭圆的离心率为
B．
C．
D．
与双曲线
有相同的焦点, 则m的值为（
）
B. 
C.
D．
与双曲线
有相同的焦点，则a的值为
B．
C．4 D．