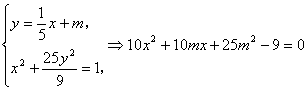题目内容
设A、B为椭圆
(a＞0)上的两点，F2为右焦点，若|AF2|+|BF2|=
a，且A、B的中点P到左准线的距离为
．
(1)求该椭圆方程；
(2)适合题设条件的直线AB的斜率是否可能等于
，若可能求出该直线AB的方程；若不可能，请说明理由．
答案：
解析：
解析：
(2)假设存在直线AB， 可设直线AB的方程为 则A、B的中点P的坐标为( 由 设A(x1，y1)、B(x2，y2)， ∵ D=100m2-40(25m2-9)＞0， ∴ 又 将 D =135＞0． 因此存在斜率为
|
)
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、命题“Ex∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1≥0” | ||||||||
| B、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” | ||||||||
C、设A、B为两个定点，k为非零常数，|
| ||||||||
D、命题：“过定圆C上一定点A作圆的动弦AB，设O为坐标原点，若
|
(a
a
=k，则动点P的轨迹为双曲线；②过定圆C上一定点A作该圆的动弦AB，O为坐标原点.若
=
（
），则动点P的轨迹为椭圆；③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率；④双曲线
=1与椭圆
=1有相同的焦点.