题目内容
已知函数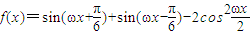 ,其中ω是使f(x)能在
,其中ω是使f(x)能在 处取得最大值时的最小正整数.(Ⅰ)求ω的值;
处取得最大值时的最小正整数.(Ⅰ)求ω的值;(Ⅱ)设△ABC的三边a,b,c满足b2=ac且边b所对的角θ的取值集合为A,当x∈A时,求f(x)的值域.
【答案】分析:(Ⅰ)利用两角和与差的余弦、正弦函数以及二倍角公式公式,化简函数f(x)=sin(ωx+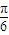 )+sin(ωx-
)+sin(ωx-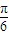 )-2cos2
)-2cos2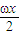
为:f(x)= ,然后利用在
,然后利用在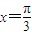 处取得最大值,求出最小正整数ω的值.
处取得最大值,求出最小正整数ω的值.
(Ⅱ)设△ABC的三边a,b,c满足b2=ac,利用余弦定理、基本不等式求出a=c,推出θ的范围,利用三角函数的有界性,求f(x)的值域.
解答:解:(Ⅰ)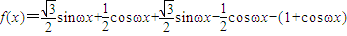 =
=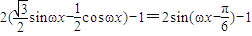
由题意得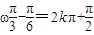 ,k∈Z,得ω=6k+2,k∈Z
,k∈Z,得ω=6k+2,k∈Z
当k=0时,最小正整数ω的值为2,故ω=2.
(Ⅱ)因b2=ac且b2=a2+c2-2accosθ
则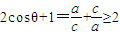 当且仅当
当且仅当 ,a=c时,等号成立
,a=c时,等号成立
则 ,又因θ∈(0,π),则
,又因θ∈(0,π),则 ,即
,即
由①知: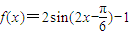
因 ,则
,则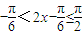 ,
,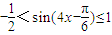 -2<f(x)≤1,
-2<f(x)≤1,
故函数f(x)的值域为:(-2,1].
点评:本题是基础题,考查两角和与差的正弦函数、余弦函数以及二倍角的应用,函数的性质,最值的求法,处理相关的多个问题时,前一问的解答是后边解答的依据,考查学生的细心程度,计算能力.
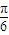 )+sin(ωx-
)+sin(ωx-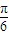 )-2cos2
)-2cos2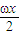
为:f(x)=
 ,然后利用在
,然后利用在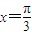 处取得最大值,求出最小正整数ω的值.
处取得最大值,求出最小正整数ω的值.(Ⅱ)设△ABC的三边a,b,c满足b2=ac,利用余弦定理、基本不等式求出a=c,推出θ的范围,利用三角函数的有界性,求f(x)的值域.
解答:解:(Ⅰ)
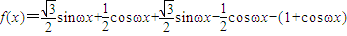 =
=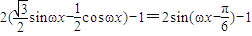
由题意得
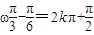 ,k∈Z,得ω=6k+2,k∈Z
,k∈Z,得ω=6k+2,k∈Z当k=0时,最小正整数ω的值为2,故ω=2.
(Ⅱ)因b2=ac且b2=a2+c2-2accosθ
则
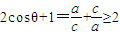 当且仅当
当且仅当 ,a=c时,等号成立
,a=c时,等号成立则
 ,又因θ∈(0,π),则
,又因θ∈(0,π),则 ,即
,即
由①知:
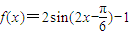
因
 ,则
,则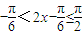 ,
,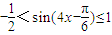 -2<f(x)≤1,
-2<f(x)≤1,故函数f(x)的值域为:(-2,1].
点评:本题是基础题,考查两角和与差的正弦函数、余弦函数以及二倍角的应用,函数的性质,最值的求法,处理相关的多个问题时,前一问的解答是后边解答的依据,考查学生的细心程度,计算能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
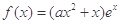 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.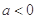 时,解不等式
时,解不等式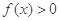 ;
;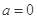 时,求正整数k的值,使方程
时,求正整数k的值,使方程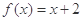 在[k,k+1]上有解;
在[k,k+1]上有解;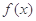 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求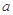 的取值范围.
的取值范围.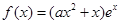 ,其中e是自然数的底数,
,其中e是自然数的底数,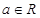 。
。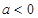 时,解不等式
时,解不等式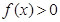 ;
;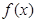 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求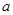 的取值范围;
的取值范围;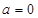 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程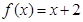 在[k,k+1]上有解。
在[k,k+1]上有解。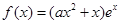 ,其中e是自然数的底数,
,其中e是自然数的底数,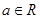 .
.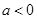 时,解不等式
时,解不等式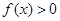 ;
; 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程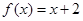 在[k,k+1]上有解;
在[k,k+1]上有解;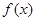 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求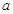 的取值范围.
的取值范围.