题目内容
函数![]() 的定义域为
的定义域为![]() (
(![]() 为实数).
为实数).
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
(3)讨论函数![]() 在
在![]()
![]() 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时![]() 的值.
的值.
解:(1)显然函数![]() 的值域为
的值域为![]() ;
;
(2)若函数![]() 在定义域上是减函数,
在定义域上是减函数,
则任取![]()
![]() 且
且![]() 都有
都有![]() 成立,
成立,
即![]() 只要
只要![]() 即可,
即可,
由![]()
![]() ,故
,故![]() ,所以
,所以![]() ,
,
故![]() 的取值范围是
的取值范围是![]() ;
;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上单调增,无最小值,
上单调增,无最小值,
当![]() 时取得最大值
时取得最大值![]() ;
;
由(2)得当![]() 时,函数
时,函数![]() 在
在![]() 上单调减,无最大值,
上单调减,无最大值,
当![]() 时取得最小值
时取得最小值![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增,无最大值,
上单调增,无最大值,
当![]() 时取得最小值
时取得最小值![]() .
.

练习册系列答案
相关题目
 :关于
:关于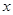 的方程
的方程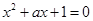 无实根;命题
无实根;命题 :函数
:函数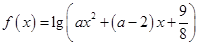 的定义域为
的定义域为 ,若命题"p或q”是真命题,“p且q”是假命题,求实数a的取值范围.
,若命题"p或q”是真命题,“p且q”是假命题,求实数a的取值范围. 的定义域为[a,b].
的定义域为[a,b]. ,若对任意的
,若对任意的 ,总存在
,总存在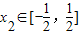 ,使得f(x2)=g(x1)成立,求实数m的取值范围.
,使得f(x2)=g(x1)成立,求实数m的取值范围.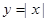 与函数
与函数 表示同一个函数;
表示同一个函数; 的图像可由
的图像可由 的图像向上平移1个单位得到;
的图像向上平移1个单位得到; 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 ;
; 是在区间
是在区间 上图象连续的函数,且
上图象连续的函数,且 ,则方程
,则方程 在区间
在区间