Question

已知数列{a_n}中,a₁=1,a_n+1a_n-1=a_na_n-1+a_n²(n∈N^*,n≥2),且=kn+1,n∈N^*.

(1)求证:k=1;

(2)设b_n=(x≠0),f(x)是数列{b_n}的前n项和,求f(x)的解析式;

(3)求证:不等式f(2)＜3ⁿ对n∈N^*恒成立.

Answer 1

(1)证明:∵=kn+1,故=a₂=k+1.

又∵a₁=1,a_n+1a_n-1=a_na_n-1+a_n²(n∈N^*,n≥2),

则a₃a₁=a₂a₁+a₂²,即=a₂+1.又=2k+1,

∴a₂=2k.

∴k+1=a₂=2k.∴k=1.

(2)解:=n+1,

a_n=··…··a₁=n·(n-1)·…·2·1=n!

∴b_n=nx^n-1.

∴当x=1时,f(x)=f(1)=1+2+3+…+n=;

当x≠1时,f(x)=1+2x+3x²+…+nx^n-1.①

①乘x,得xf(x)=x+2x²+3x³+…+(n-1)x^n-1+nxⁿ,②

①-②,得(1-x)f(x)=1+x+x²+…+x^n-1-nxⁿ=-nxⁿ,

∴f(x)=.

综上所述:f(x)=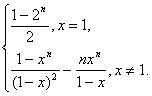

(3)证明:∵f(2)==(n-1)2ⁿ+1,

(i)易验证当n=1,2,3时不等式成立;

(ii)假设n=k(k≥3)不等式成立,即3^k＞(k-1)2^k+1,

两边乘以3,得3^k+1＞3(k-1)2^k+3=k·2^k+1+1+3(k-1)2^k-k2^k+1+2.

又∵3(k-1)2^k-k·2^k+1+2=2^k(3k-3-2k)+2=(k-3)2^k+2＞0,

∴3^k+1＞k·2^k+1+1+3(k-1)2^k-k2^k+1+2＞k·2^k+1+1,

即n=k+1时不等式成立.

综合(i)(ii),不等式对n∈N^*恒成立.