题目内容
(2013•韶关三模)已知数列{an}中,a1=1,an+1an-1=anan-1+an2(n∈N+,n≥2),且
=kn+1,
(Ⅰ)求证:k=1;
(Ⅱ)设g(x)=
,f(x)是数列{g(x)}的前n项和,求f(x)的解析式;
(Ⅲ)求证:不等式f(2)<
g(3)对n∈N+恒成立.
| an+1 |
| an |
(Ⅰ)求证:k=1;
(Ⅱ)设g(x)=
| anxn-1 |
| (n-1)! |
(Ⅲ)求证:不等式f(2)<
| 3 |
| n |
分析:(I)利用an+1an-1=anan-1+
中n=2,及a1=1,得到a3a1=a2a1+a22,即
=a2+1;再利用
=kn+1,得到
=2k+1,
=k+1即可证明.
(II)利用“累成求积”即可得到g(x),再利用“错位相减法”及等差数列与等比数列的前n项和公式即可得出f(x);
(III)利用(2)中f(x)的表达式,取x=2,则f(2)=
-
=(n-1)•2n+1,又
g(3)=3n,利用数学归纳法证明:不等式f(2)<
g(3)对n∈N+恒成立.
| a | 2 n |
| a3 |
| a2 |
| an+1 |
| an |
| a3 |
| a2 |
| a2 |
| a1 |
(II)利用“累成求积”即可得到g(x),再利用“错位相减法”及等差数列与等比数列的前n项和公式即可得出f(x);
(III)利用(2)中f(x)的表达式,取x=2,则f(2)=
| 1-2n |
| (1-2)2 |
| n•2n |
| 1-2 |
| 3 |
| n |
| 3 |
| n |
解答:(I)证明:∵
=kn+1,
∴
=a2=k+1,
又∵a1=1,an+1an-1=anan-1+an2(n∈N+,n≥2)
则a3a1=a2a1+a22,即
=a2+1,又
=2k+1,∴a2=2k.
∴k+1=2k,解得k=1.
(2)∵
=n+1,∴an=
•
…
•a1=n•(n-1)…2•1=n!
∵g(x)=
=nxn-1
∴当x=1时,f(x)=f(1)=1+2+3+…+n=
,
当x≠1时,f(x)=1+2x+3x2+…+nxn-1.
得xf(x)=x+2x2+3x3+…+(n-1)xn-1+nxn
两式相减得(1-x)f(x)=1+x+x2+…+xn-1-nxn=
-nxn
∴f(x)=
-
综上所述:f(x)=
.
(3)利用(2)中f(x)的表达式,取x=2,
则f(2)=
-
=(n-1)•2n+1,
又
g(3)=3n,下面利用数学归纳法证明:不等式f(2)<
g(3)对n∈N+恒成立.
易验证当n=1,2,3时不等式恒成立;
假设n=k(k≥3),不等式成立,即3k>(k-1)2k+1
两边乘以3得:3k+1>3(k-1)2k+3=k•2k+1+1+3(k-1)2k-k2k+1+2
又因为3(k-1)2k-k•2k+1+2=2k(3k-3-2k)+2=(k-3)2k+2>0
所以3k+1>k•2k+1+1+3(k-1)2k-k2k+1+2>k•2k+1+1
即n=k+1时不等式成立.
故不等式恒成立.
| an+1 |
| an |
∴
| a2 |
| a1 |
又∵a1=1,an+1an-1=anan-1+an2(n∈N+,n≥2)
则a3a1=a2a1+a22,即
| a3 |
| a2 |
| a3 |
| a2 |
∴k+1=2k,解得k=1.
(2)∵
| an+1 |
| an |
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
∵g(x)=
| anxn-1 |
| (n-1)! |
∴当x=1时,f(x)=f(1)=1+2+3+…+n=
| n(n+1) |
| 2 |
当x≠1时,f(x)=1+2x+3x2+…+nxn-1.
得xf(x)=x+2x2+3x3+…+(n-1)xn-1+nxn
两式相减得(1-x)f(x)=1+x+x2+…+xn-1-nxn=
| 1-xn |
| 1-x |
∴f(x)=
| 1-xn |
| (1-x)2 |
| nxn |
| 1-x |
综上所述:f(x)=
|
(3)利用(2)中f(x)的表达式,取x=2,
则f(2)=
| 1-2n |
| (1-2)2 |
| n•2n |
| 1-2 |
又
| 3 |
| n |
| 3 |
| n |
易验证当n=1,2,3时不等式恒成立;
假设n=k(k≥3),不等式成立,即3k>(k-1)2k+1
两边乘以3得:3k+1>3(k-1)2k+3=k•2k+1+1+3(k-1)2k-k2k+1+2
又因为3(k-1)2k-k•2k+1+2=2k(3k-3-2k)+2=(k-3)2k+2>0
所以3k+1>k•2k+1+1+3(k-1)2k-k2k+1+2>k•2k+1+1
即n=k+1时不等式成立.
故不等式恒成立.
点评:本题综合考查了等差数列与等比数列的前n项和公式、“累成求积”、“错位相减法”,及其数学归纳法,需要较强的推理能力和计算能力.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
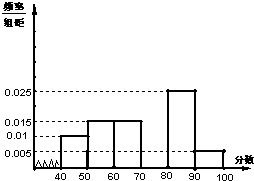 (2013•韶关三模)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(2013•韶关三模)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: