题目内容
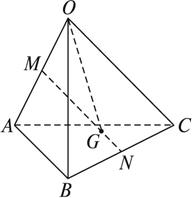
如图所示,OA、OB、OC为不共面的三条射线,点A1、B1、C1分别是OA、OB、OC上的点,且![]() =
=![]() =
=![]() 成立.
成立.
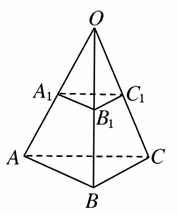
求证:△A1B1C1∽△ABC.
[分析] 由初中所学平面几何知识,可证明两内角对应相等,进而证明两个三角形相似.
[证明] 在△OAB中,
∵![]() =
=![]() ,∴A1B1∥AB.
,∴A1B1∥AB.
同理可证A1C1∥AC,B1C1∥BC.
∴∠C1A1B1=∠CAB,∠A1B1C1=∠ABC.
∴△A1B1C1∽△ABC.
[反思] 在立体几何中,常利用等角定理来证明两个角相等.此时要注意观察这两个角的方向必须相同,且能证明它们的两边对应平行.

练习册系列答案
相关题目
 函数y=tan(
函数y=tan(| π |
| 4 |
| π |
| 2 |
| OB |
| OA |
| OB |
| A、-4 | B、2 | C、-2 | D、4 |
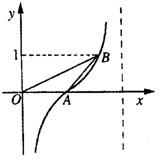
 (2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于
(2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于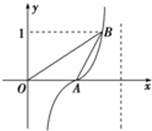 函数y=tan(
函数y=tan(