题目内容
已知向量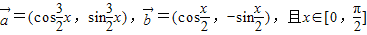 .
.(1)求
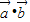 及
及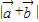 ;
;(2)若
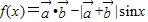 ,试求f(x)的值域.
,试求f(x)的值域.
【答案】分析:(1)利用两个向量数量积公式求得 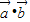 =cos2x,求出
=cos2x,求出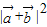 的值 可得
的值 可得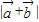 的值.
的值.
(2)利用二倍角公式及辅助角公式化简f(x)的解析式为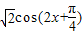 ,再根据
,再根据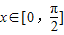 求出函数f(x)的值域.
求出函数f(x)的值域.
解答:解:(1)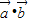 =cos
=cos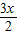 cos
cos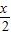 +sin
+sin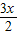 sin
sin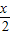 =cos(
=cos( 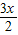 +
+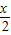 )=cos2x.
)=cos2x.
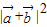 =
=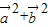 +2
+2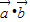 =2+2cos2x.
=2+2cos2x.
由于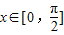 ,
,
∴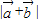 =
=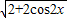 =
=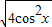 =2cosx.
=2cosx.
(2)∵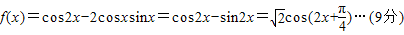 ,
,
又∵ ,∴
,∴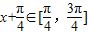 ,
,
∴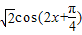
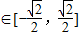 ,
,
故函数f(x)的值域是[-1,1].…(12分)
点评:本题主要考查两个向量数量积公式的应用,求向量的模的方法,余弦函数的定义域和值域,属于基础题.
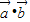 =cos2x,求出
=cos2x,求出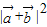 的值 可得
的值 可得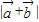 的值.
的值.(2)利用二倍角公式及辅助角公式化简f(x)的解析式为
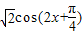 ,再根据
,再根据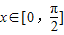 求出函数f(x)的值域.
求出函数f(x)的值域.解答:解:(1)
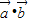 =cos
=cos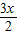 cos
cos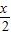 +sin
+sin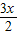 sin
sin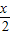 =cos(
=cos( 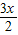 +
+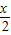 )=cos2x.
)=cos2x.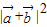 =
=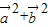 +2
+2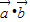 =2+2cos2x.
=2+2cos2x.由于
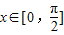 ,
,∴
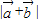 =
=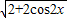 =
=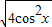 =2cosx.
=2cosx.(2)∵
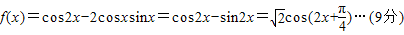 ,
,又∵
 ,∴
,∴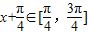 ,
,∴
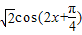
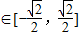 ,
,故函数f(x)的值域是[-1,1].…(12分)
点评:本题主要考查两个向量数量积公式的应用,求向量的模的方法,余弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
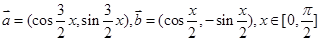 ,
,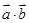 及
及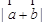 ;
;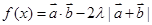 的最小值为
的最小值为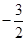 ,求
,求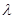 的值.
的值.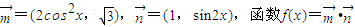 .
.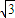 ,且a>b,求a,b的值.
,且a>b,求a,b的值.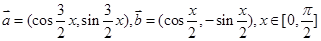 ,
,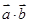 及
及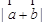 ;
;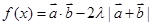 的最小值为
的最小值为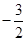 ,求
,求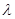 的值.
的值.