题目内容
已知向量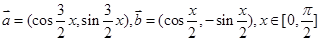 ,
,
(1)求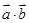 及
及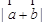 ;
;
(2)若函数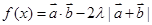 的最小值为
的最小值为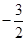 ,求
,求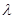 的值.
的值.
(1)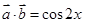
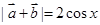 (2)
(2)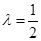
解析试题分析:(1)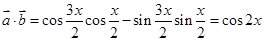
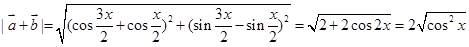
∵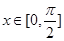 ,∴
,∴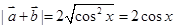
(2)由(1)可得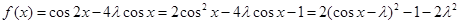
∵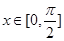 ,∴
,∴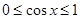
①当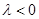 时,当且仅当
时,当且仅当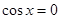 时,
时, 取得最小值-1,不合题意;
取得最小值-1,不合题意;
②当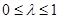 时,当且仅当
时,当且仅当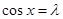 时,
时, 取得最小值
取得最小值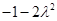 ,由已知
,由已知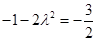 ,解得
,解得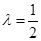
③当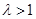 时,当且仅当
时,当且仅当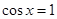 ,
, 取得最小值
取得最小值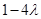 ,由已知
,由已知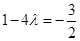 ,解得
,解得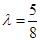 ,这与
,这与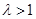 矛盾.
矛盾.
综上所述,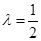 即为所求.
即为所求.
考点:平面向量数量积的运算;向量的模;数量积表示两个向量的夹角;同角三角函数基本关系的运用.
点评:本题考查向量的数量积公式、向量模的坐标公式、三角形的余弦定理、三角函数的二倍角公式、整体思想求三角函数的最值

练习册系列答案
相关题目
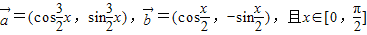 .
.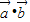 及
及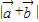 ;
;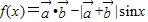 ,试求f(x)的值域.
,试求f(x)的值域.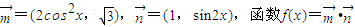 .
.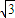 ,且a>b,求a,b的值.
,且a>b,求a,b的值.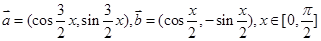 ,
,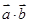 及
及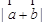 ;
;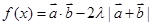 的最小值为
的最小值为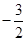 ,求
,求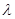 的值.
的值.