题目内容
已知正项数列{an}中,a1=1,且log3an,log3an+1是方程x2 (2n
(2n 1)x+bn=0的两个实根.
1)x+bn=0的两个实根.
(1)求a2,b1;
(2)求数列{an}的通项公式;
(3)若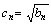 ,
,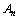 是
是 前
前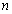 项和,
项和, 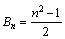 ,当
,当 时,试比较
时,试比较 与
与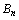 的大小.
的大小.
【答案】
(1) ,
, ;(2)
;(2)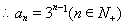 ;(Ⅲ)当
;(Ⅲ)当 时,
时,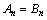 ,当
,当 时,
时,  .
.
【解析】
试题分析:(1)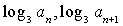 是方程
是方程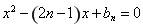 的两个实根,有根与系数关系可得,
的两个实根,有根与系数关系可得, ,
, ,求
,求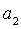 ,
,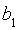 的值,可利用对数的运算性质,及已知
的值,可利用对数的运算性质,及已知 ,只需令
,只需令 即可求出
即可求出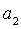 ,
,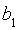 的值;(2)求数列
的值;(2)求数列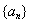 的通项公式,由
的通项公式,由 得,
得,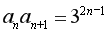 ,所以
,所以 ,即
,即 ,得数列
,得数列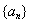 的奇数项和偶数项分别是公比为9的等比数列,分别写出奇数项和偶数项的通项公式,从而可得数列
的奇数项和偶数项分别是公比为9的等比数列,分别写出奇数项和偶数项的通项公式,从而可得数列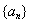 的通项公式;(Ⅲ)若
的通项公式;(Ⅲ)若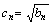 ,
, 是
是 前
前 项和,
项和,  ,当
,当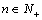 时,试比较
时,试比较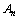 与
与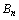 的大小,此题关键是求数列
的大小,此题关键是求数列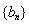 的通项公式,由(1)可知
的通项公式,由(1)可知 ,可得
,可得 ,当
,当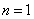 时,
时, 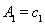 =0,
=0,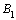 =0,得
=0,得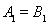 ,当
,当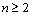 时,有基本不等式可得
时,有基本不等式可得 ,从而可得
,从而可得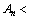 0+
0+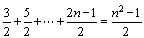 =
=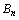 ,即可得结论.
,即可得结论.
试题解析:(1)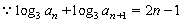 ,
,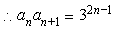
当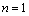 时,
时,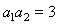 ,
, ,
,
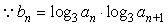 ,
,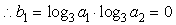
(2)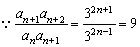 ,
,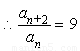 ,
,
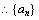 的奇数项和偶数项分别是公比为9的等比数列.
的奇数项和偶数项分别是公比为9的等比数列.
 ,
,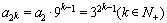 ,
,

(3) 

当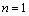 时,
时, 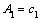 =0,
=0,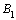 =0,
=0, .
.
当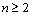 时,
时,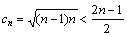
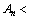 0+
0+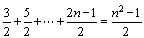 =
=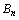
综上,当 时,
时,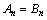 ,当
,当 时,
时,  .
.
或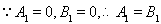
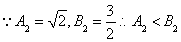

猜测 时,
时, 用数学归纳法证明
用数学归纳法证明
①当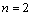 时,已证
时,已证
②假设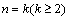 时,
时, 成立
成立
当 时,
时,

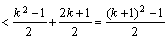

即 时命题成立
时命题成立
根据①②得当 时,
时,
综上,当 时,
时,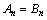 ,当
,当 时,
时, 
考点:求数列的通项公式,数列求和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目